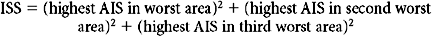INJURY DESCRIPTION AND SCORING: CONCEPTUAL BACKGROUND

Injury scoring is a process that reduces the myriad complexities of a clinical situation to a single number. In this process information is necessarily lost. What is gained is a simplification that facilitates data manipulation and makes objective prediction possible. The expectation that prediction will be improved by scoring systems is unfounded, however, since when ICU scoring systems have been compared to clinical acumen, the clinicians usually perform better.^4,5

Clinical trauma research is made difficult by the seemingly infinite number of possible anatomic injures, and this is the first problem we must confront. Injury description can be thought of as the process of subdividing the continuous landscape of human injury into individual, well-defined injuries. Fortunately for this process, the human body tends to fail structurally in consistent ways. Le Fort⁶ discovered that the human face usually fractures in only three patterns despite a wide variety of traumas, and this phenomenon is true for many other parts of the body. The common use of eponyms to describe apparently complex orthopedic injuries underscores the frequency with which bones fracture in predictable ways. Nevertheless, the total number of possible injuries is large. The Abbreviated Injury Scale is now in its fifth edition (AIS 2005) and includes descriptions of more than 2000 injuries (increased from 1395 in AIS 1998). The International Classification of Diseases, Ninth Revision (ICD-9) also devotes almost 2000 codes to traumatic injuries. Moreover, most specialists could expand by several-fold the number of possible injuries. However, a scoring system detailed enough to satisfy all specialists would be so demanding in practice that it would be impractical for nonspecialists. Injury dictionaries thus represent an unavoidable compromise between clinical detail and pragmatic application.

Although an “injury” is usually thought of in anatomic terms, physiologic injuries at the cellular level, such as hypoxia or hemorrhagic shock, are also important. Not only does physiologic impairment figure prominently in the injury description process used by emergency paramedical personnel for triage, but such descriptive categories are crucial if injury description is to be used for accurate prediction of outcome. Thus, the outcome after splenic laceration hinges more on the degree and duration of hypotension than on degree of structural damage to the spleen itself. Because physiologic injuries are by nature evanescent, changing with time and therapy, reliable capture of this type of data is problematic.

The ability to describe injuries consistently on the basis of a single descriptive dictionary guarantees that similar injuries will be classified as such. However, in order to compare different injuries, a scale of severity is required. Severity is usually interpreted as the likelihood of a fatal outcome; however, length of stay in an intensive care unit, length of hospital stay, extent of disability, or total expense that is likely to be incurred could each be considered measures of severity as well.

In the past, severity measures for individual injuries have generally been assigned by experts. Ideally, however, these values should be objectively derived from injury-specific data that is now available in large data bases. Importantly, the severity of an injury may vary with the outcome that is being contemplated. Thus, a gunshot wound to the aorta may have a high severity when mortality is the outcome measure, but a low severity when disability is the outcome measure. (That is, if the patient survives he or she is likely to recover quickly.) A gunshot wound to the femur might be just the reverse in that it infrequently results in death but often causes prolonged disability.

Although it is a necessary first step to rate the severity of individual injuries, comparisons between patients or groups of patients is of greater interest. Because patients typically have more than a single injury, the severity of several individual injuries must be combined in some way to produce a single overall measure of injury severity. Although several mathematical approaches of combining separate injuries into a single score have been proposed, it is uncertain which of these formulas is most correct. The severity of the single worst injury, the product of the severities of all the injuries a patient has sustained, the sum of the squared values of severities of a few of the injuries a patient has sustained, have all been proposed, and other schemes are likely to emerge. The problem is made still more complex by the possibility of interactions between injuries. We will return to this fundamental but unresolved issue later.

As noted, anatomic injury is not the sole determinant of survival. Physiologic derangement and patient reserve also play crucial roles. A conceptual expression to describe the role of anatomic injury, physiologic injury, and physiologic reserve in determining outcome might be stated as follows:

Our task is thus twofold: First, we must define summary measures of anatomic injury, physiologic injury, and patient reserve. Second, we must devise a mathematical expression combining these predictors into a single prediction of outcome, which for consistency will always be an estimated probability of survival. We will consider both of these tasks in turn. However, before we can consider various approaches to outcome prediction, we must briefly discuss the statistical tools that are used to measure how well predictive models succeed in the tasks of measuring injury severity and in separating survivors from nonsurvivors.

TESTING A TEST: STATISTICAL MEASURES OF PREDICTIVE ACCURACY AND POWER

Most clinicians are comfortable with the concepts of sensitivity and specificity when considering how well a laboratory test predicts the presence or absence of a disease. Sensitivity and specificity are inadequate for the thorough evaluation of tests, however, because they depend on an arbitrary cut-point to define “positive” and “negative” results. A better overall measure of the discriminatory power of a test is the area under the receiver operation characteristic (ROC) curve. Formally defined as the area beneath a graph of sensitivity (true positive proportion) graphed against 1 – specificity (false positive proportion), the ROC statistic can more easily be understood as the proportion of correct discriminations a test makes when confronted with all possible comparisons between diseased and nondiseased individuals in the data set. In other words, imagine that a survivor and a nonsurvivor are randomly selected by a blindfolded researcher, and the scoring system of interest is used to try to pick the survivor. If we repeat this trial many times (e.g., 10,000 or 100,000 times), the area under the ROC curve will be the proportion of correct predictions. Thus, a test that always distinguishes a survivor from a nonsurvivor correctly has an ROC of 1, whereas a test that picks the survivor no more often than would be done by chance has an ROC of 0.5.

A second salutary property of a predictive model is that it has clarity of classification. That is, if a rule classifies a patient with an estimated chance of survival of 0.5 or greater to be a survivor, then ideally the model should assign survival probabilities near 0.5 to as few patients as possible and values close to 1 (death) or 0 (survival) to as many patients as possible. A rule with good discriminatory power will typically have clarity of classification for a range of cut-off values.

A final property of a good scoring system is that it is well calibrated, that is, reliable. In other words, a predictive scoring system that is well calibrated should perform consistently throughout its entire range, with 50% of patients with a 0.5 predicted mortality actually dying, and 10% or patients with a 0.1 predicted mortality actually dying. Although this is a convenient property for a scoring system to have, it is not a measure of the actual predictive power of the underlying model and predictor variables. In particular, a well-calibrated model does not have to produce more accurate predictions of outcome than a poorly calibrated model. Calibration is best thought of as a measure of how well a model fits the data, rather than how well a model actually predicts outcome. As an example of the malleability of calibration, Figure 2A and B displays the calibration of a single ICD-9 Injury Severity Score (ICISS) (discussed later), first as the raw score and then as a simple mathematical transformation of the raw score. Although the addition of a constant and a fraction of the score squared add no information and does not change the discriminatory power based on ROC, the transformed score presented in Figure 2B is dramatically better calibrated. Calibration is commonly evaluated using the Hosmer Lemeshow (HL) statistic. This statistic is calculated by first dividing the data set into 10 equal deciles (by count or value) and then comparing the predicted number of survivors in each decile to the actual number of survivors. The result is evaluated as a chi-square test. A high (p>0.05) value implies that the model is well calibrated, that is, it is accurate. Unfortunately, the HL statistic is sensitive to the size of the data set, with very large data sets uniformly being declared “poorly calibrated.” Additionally, the creators of the HL statistic have noted that its actual value may depend on the arbitrary groupings used in its calculation,⁷ and this further diminishes the HL statistic’s appeal as a general measure of reliability.

Figure 2 (A) Survival as a function of Injury Severity Scores (ISS). One-half of valid ISS score values are below 25 due to the sum of squares definition of ISS. Because the data set is spread over 44 ISS scores, and higher scores occur less often, error bars for higher ISS scores are wider than for lower ISS values (691,973 patients from the NTDB). (B) ISS presented as paired histograms of survivors (above) and nonsurvivors (below). Note that only the 44 possible ISS scores are represented. In general, survivors tend to have lower ISS scores. Some ISS scores are dramatically more common, in part because these scores result from two or more combinations of AIS severity scores (691,973 patients from the NTDB).

In sum, the ROC curve area is a measure of how well a model distinguishes survivors from nonsurvivors, whereas the HL statistic is a measure of how carefully a model has been mathematically fitted to the data. In the past, the importance of the HL statistic has been overstated and even used to commend one scoring system (A Severity Characterization of Trauma [ASCOT]) over another of equal discriminatory power (TRISS). This represents a fundamental misapplication of the HL statistic. Overall, we believe much less emphasis should be placed on the HL statistic.

The success of a model in predicting mortality is thus measured in terms of its ability to discriminate survivors from nonsurvivors (ROC statistic) and its calibration (HL statistic). In practice, however, we often wish to compare two or more models rather than simply examine the performance of a single model. The procedure for model selection is a sophisticated statistical enterprise that has not yet been widely applied to trauma outcome models. One promising avenue is an information theoretic approach in which competing models are evaluated based on their estimated distance from the true (but unknown) model in terms of information loss. While it might seem impossible to compare distances to an unknown correct model, such comparisons can be accomplished by using the Akaike information criterion (AIC)⁸ and related refinements.

Two practical aspects of outcome model building and testing are particularly important. First, a model based on a data set usually performs better when it is used to predict outcomes for that data set than other data sets. This is not surprising, because any unusual features of that data set will have been incorporated, at least partially, into the model under consideration. The second, more subtle, point is that the performance of any model depends on the data evaluated. A data set consisting entirely of straightforward cases (i.e., all patients are either trivially injured and certain to survive or overwhelmingly injured and certain to die) will make any scoring system seem accurate. But a data set in which every patient is gravely but not necessarily fatally injured is likely to cause the scoring system to perform no better than chance. Thus, when scoring systems are being tested, it is important first that they be developed in unrelated data sets and second that they be tested against data sets typical of those expected when the scoring system is actually used. This latter requirement makes it extremely unlikely that a universal equation can be developed, because factors not controlled for by the prediction model are likely to vary among trauma centers.

MEASURING ANATOMIC INJURY

Measurement of anatomic injury requires first a dictionary of injuries, second a severity for each injury, and finally a rule for combining multiple injuries into a single severity score. The first two requirements were addressed in 1971 with the publication of the first AIS manual. Although this initial effort included only 73 general injuries and did not address penetrating trauma, it did assign a severity to each injury varying from 1 (minor) to 6 (fatal). No attempt was made to create a comprehensive list of injuries, and no mechanism to summarize multiple injuries into a single score was proposed.

This inability to summarize multiple injuries occurring in a single patient soon proved problematic and was addressed by Baker and colleagues in 1974 when they proposed the ISS. This score was defined as the sum of the squares of the highest AIS grade in each of the three (of six) most severely injured body areas:

Because each injury was assigned an AIS severity from 1 to 6, the ISS could assume values from 0 (uninjured) to 75 (severest possible injury). A single AIS severity of 6 (fatal injury) resulted in an automatic ISS of 75. This scoring system was tested in a group of 2128 automobile accident victims. Baker concluded that 49% of the variability in mortality was explained by this new score, a substantial improvement over the 25% explained by the previous approach of using the single worst-injury severity.

Both the AIS dictionary and the ISS score have enjoyed considerable popularity over the past 30 years. The fifth revision of the AIS⁹ has recently been published, and now includes over 2000 individual injury descriptors. Each injury in this dictionary is assigned a severity from 1 (slight) to 6 (unsurvivable), as well as a mapping to the Functional Capacity Index (a quality-of-life measure).¹⁰ The ISS has enjoyed even greater success—it is virtually the only summary measure of trauma in clinical or research use, and has not been modified in the 30 years since its invention.

Despite their past success, both the AIS dictionary and the ISS score have substantial shortcomings. The problems with AIS are twofold. First, the severities for each of the 2000 injuries are consensus derived from committees of experts and not simple measurements. Although this approach was necessary before large databases of injuries and outcomes were available, it is now possible to accurately measure the severity of injuries on the basis of actual outcomes. Such calculations are not trivial, however, because patients typically have more than a single injury, and untangling the effects of individual injuries is a difficult mathematical exercise. Using measured severities for injuries would correct the inconsistent perceptions of severity of injury in various body regions first observed by Beverland and Rutherford¹¹ and later confirmed by Copes et al.¹² A second difficulty is that AIS scoring is expensive, and therefore is done only in hospitals with a zealous commitment to trauma. As a result, the experiences of most non-trauma center hospitals are excluded from academic discourse, thus making accurate demographic trauma data difficult to obtain.

The ISS has several undesirable features that result from its weak conceptual underpinnings. First, because it depends on the AIS dictionary and severity scores, the ISS is heir to all the difficulties outlined previously. But the ISS is also intrinsically flawed in several ways. By design, the ISS allows a maximum of three injuries to contribute to the final score, but the actual number is often fewer. Moreover, because the ISS allows only one injury per body region to be scored, the scored injuries are often not even the three most severe injuries. By considering less severe injuries, ignoring more severe injuries, and ignoring many injuries altogether, the ISS loses considerable information. Baker herself proposed a modification of the ISS, the new ISS (NISS¹³), which was computed from the three worst injuries, regardless of the body region in which they occurred. Unfortunately, the NISS did not improve substantially upon the discrimination of ISS.

The ISS is also flawed in a mathematical sense. Although it is usually handled statistically as a continuous variable, the ISS can assume only integer values. Further, although its definition implies that the ISS can at least assume all integer values throughout its range of 0 to 75, because of its curious sum-of-one (or two or three) square construction, many integer values can never occur. For example, 7 is not the sum of any three squares, and therefore can never be an ISS score. In fact, only 44 of the values in the range of ISS can be valid ISS scores, and half of these are concentrated between 0 and 26. As a final curiosity, some ISS values are the result of one, two, or as many as 28 different AIS combinations. Overall, the ISS is perhaps better thought of as a procedure that maps the 84 possible combinations of three or fewer AIS injuries into 44 possible scores that are distributed between 0 and 75 in a nonuniform way.

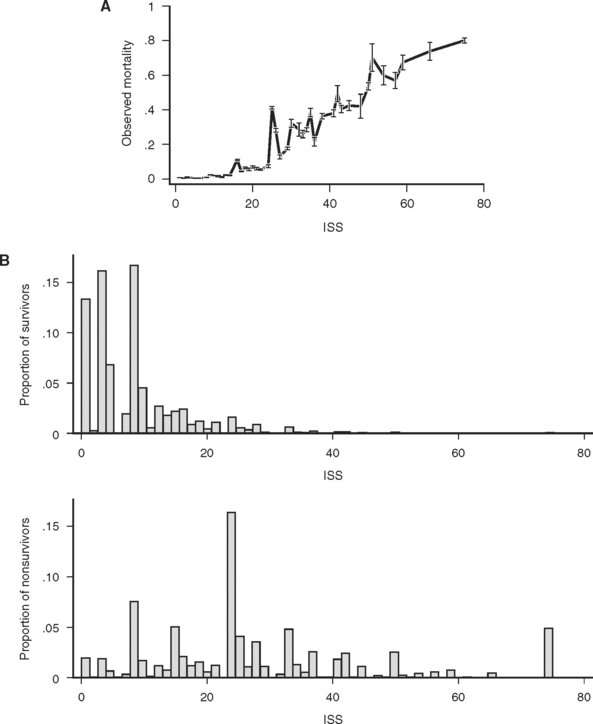
The consequences of these idiosyncrasies for the ISS are severe, as an examination of the actual mortality for each of 44 ISS scores in a large data set (691,973 trauma patients contributed to the National Trauma Data Bank [NTDB]¹⁴) demonstrates. Mortality does not increase smoothly with increasing ISS, and, more troublingly, for many pairs of ISS scores, the higher score is actually associated with a lower mortality (Figure 1A). Some of these disparities are striking: patients with ISS scores of 27 are four times less likely to die than patients with ISS scores of 25. This anomaly occurs because the injury subscore combinations that result in an ISS of 25 (5,0,0 and 4,3,0) are, on average, more likely to be fatal than the injury subscore combinations that result in and ISS of 27 (5,1,1 and 3,3,3). (Kilogo et al.¹⁵ note that 25% of ISS scores can actually be the result of two different subscore combinations, and that these subscore combinations usually have mortalities that differ by over 20%.)

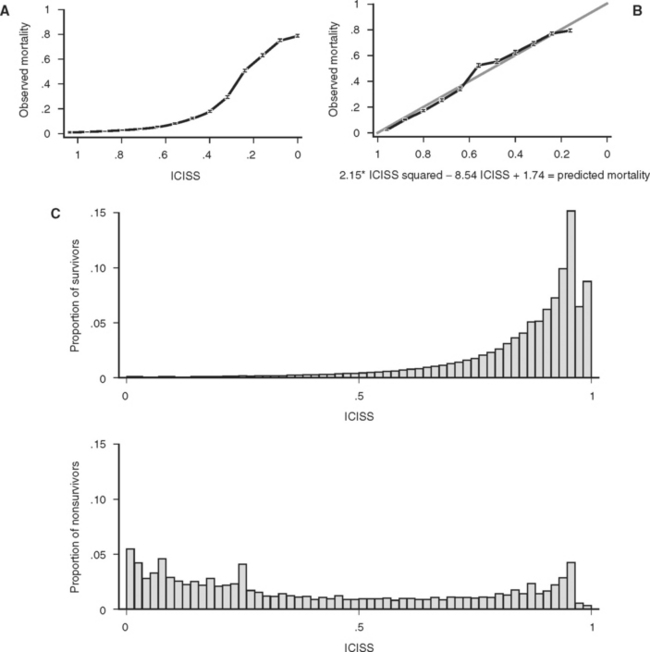
Figure 1 (A) Survival as a function of ICD-9 Injury Scoring System (ICISS) score (691,973 patients from the National Trauma Data Bank [NTDB]). (B) Survival as a function of ICISS score mathematically transformed by the addition of an ICISS² term (a “calibration curve”). Note that although this transformation does not add information (or change the discrimination [receiver operation characteristic value]) of the model, it does substantially improve the calibration of the model (691,973 patients from the NTDB). (C) ICISS scores presented as paired histograms of survivors (above) and nonsurvivors (691,973 patients from the NTDB).