Chapter 3
Gas Exchange
Zoheir Bshouty
Chapter Overview
Gas exchange involves the exchange of gases between the lung and the blood. The gases of interest are oxygen and carbon dioxide. The general objectives behind this chapter are to leave you with enough basic physiological knowledge that would enable you to identify derangements in gas exchange based on the interpretation of arterial blood gases and to try to identify the mechanism(s) leading to these derangements.
Although pH plays a certain role in interpreting arterial blood gases, when dealing with gas exchange, emphasis is on interpreting derangements in the partial pressure of arterial oxygen (PaO2) and the partial pressure of arterial carbon dioxide (PaCO2).
To help with these, some key equations will be used. The derivation of these equations is beyond the scope of this chapter but the principles used in deriving these equations will be mentioned. Equations that are useful in clinical practice are boxed.
The chapter will start with derangements in carbon dioxide followed by derangements in oxygen. The reason for this order, as you will see later, is that derangements in carbon dioxide can directly lead to derangements in oxygen, while derangements in oxygen do not affect carbon dioxide. The goal is to keep the topic as simple as possible and at the same time clinically relevant. Often, learners fail to understand the link between theory and clinical applicability; therefore, the chapter starts with two clinical scenarios that will be referred to occasionally to help maintain this link.
In this chapter and in pulmonary physiology in general, V indicates volume. Subscripts are used to identify the various types of volumes (e.g., VD for dead space). When written with a diacritic period such as V it indicates volume measured over a period of one minute (e.g., VE for minute ventilation).
The Problem
Case 1. An elderly man is brought to the Emergency Department by his daughter. He tells the resident that his chronic cough and shortness of breath have become worse in the last few days, during which time he has had periods of drowsiness and confusion. The patient is drowsy and uncooperative, blue and in obvious respiratory distress. The resident decides to take an arterial blood gas sample on room air.
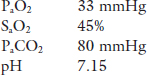
Case 2. An elderly woman presents to the outpatient clinic complaining of increased fatigue and shortness of breath on exertion that were insidious in nature and have gradually progressed over the past five years. As part of her investigation an arterial blood gas on room air is drawn with the following results:
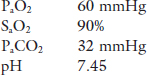
Analyzing PaO2 and PaCO2 and identifying the mechanism(s) for the gas exchange disturbances in the earlier context is the topic of this chapter.
Normal values for arterial blood gases
Textbooks often reference the following normal ranges for arterial blood gases,
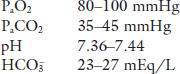
The lungs are the first link in the O2 transport chain to the tissues (for metabolism) and the last link in the CO2 transport chain (by-product of metabolism). There is no doubt that both patients have a problem getting O2 into their blood. In addition, the first patient has a problem getting rid of CO2.
As mentioned earlier, we will refer back to these two cases as new concepts are learned to maintain the link between theory and clinical practice.
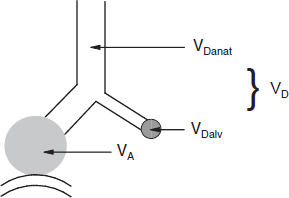
Anatomic dead space (VDanat) is the volume of all non-gas-exchanging airways from the nose (or mouth, during mouth-breathing) down to the respiratory bronchioles Fig. 1.
Alveolar dead space (VDalv) is the volume of inspired air that is delivered to alveoli in which there is no gas exchange or gas exchange is incomplete. VDalv is primarily the result of under perfusion of the affected alveoli Fig 1. VDalv is too small to be measured in healthy subjects, particularly young people, but can become large enough to interfere with alveolar ventilation (VA) in patients who have certain lung diseases, in spite high VE.
Physiologic dead space (VD) is the sum of VDanat and VDalv. VD defines the portion of each inspiration that does not equilibrate with gas pressures of the pulmonary capillary blood Fig. 1.
Fig. 1. Dead space (VD). In this figure, the white area represents anatomic dead space (VDanat), the grayed circle represents alveolar dead space (VDalv), and VD represents physiologic dead space which is the sum of VDanat and VDalv.
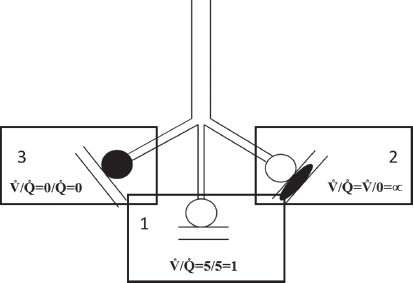
1.Alveoli that are optimally and equally ventilated and perfused (with complete equilibration of gas pressures between alveoli and capillary blood, V/Q = 1, Fig. 2 compartment 1).
2.Alveoli that are optimally ventilated but not perfused at all (“VDanat”, V/Q Fig. 2 compartment 2 = ∞)
3.Alveoli that are optimally perfused but not ventilated at all (contributing to “shunt”, V/Q Fig. 2 compartment 3 = 0)
Thus, VD is a theoretical rather than an actual volume.
Fig. 2. This figure represents the three main compartment within the lung based on the ventilation to perfusion ratio. Clear circles represent adequately ventilated alveoli (compartments 1 and 2) whereas the black filled circle represents non-ventilated alveoli (compartment 3). Similarly, the clear parallel lines represent capillaries that are perfused (compartments 1 and 3) and the parallel lines with the black ellipse (compartment 2) represents capillaries that are not perfused.
Factors affecting VDanat
Size of subject. VDanat is highly dependent on body size. A good estimate is based on body height (rather than body weight), a relationship that holds true for both children and adults.
Age. VDanat increases slightly with age. This increase is probably due to loss of elasticity (i.e., increased compliance) of airways.
Breathing pattern. VDanat increases with increasing tidal volume (VT). This is due to the increase in distending pressure that parallels the increase in VT which stretches the elastic airways as well as the lungs.
Factors affecting VDalv
Pulmonary embolism. Occlusion of pulmonary vessels creates a situation where alveoli continue to be ventilated yet unperfused, hence contributing to an increase in VDalv.
Mechanical ventilation with high Positive End-Expiratory Pressure (PEEP). Similar situation to pulmonary embolism except that pulmonary vessels are occluded by the high alveolar pressure.
The increase in VDanat is usually not enough to cause a disturbance in gas exchange. Diseases that affect gas exchange through their effect on dead space do so by increasing VDalv which, in turn, leads to an increase in VD. So, it suffices to calculate VD in order to determine whether it is contributing to a gas exchange derangement.
Calculation of VD
Why is it important to calculate VD? The answer is very simple, Dead Space ventilation (VD) is considered wasted ventilation. The larger the dead space volume, VD (or ventilation, VD) the less volume is available for adequate gas exchange (termed alveolar volume, VA, or ventilation, VA, Eq. 3.3). And, as you will see later, VA, and in turn VA, have a large impact on carbon dioxide elimination.
VE. The total amount of gas that is moved in and out of the lung per minute and is equal to the product of VT and respiratory frequency (f):

VD. The amount of gas that moves in and out of the dead space of the lung per minute and is equal to the product of VD and f:


Bohr equation. The Bohr Equation enables us to estimate VD (as a proportion of VT) using a sample of CO2 in mixed expired gas (PMECO2) and PaCO2. The derivation of this relationship is based on the laws of conservation of mass for CO2,1
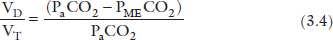
Going back to Case 1, if the patient’s PMECO2 was 36 mmHg, given a PaCO2 of 80 mmHg, the proportion of the total ventilation that is being wasted in dead space is (applying Eq. (3.4)):
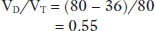
Indicating that over half of his VT is wasted on dead space. Under normal condition, at rest, VD/VT is approximately 0.3 (30%).
One of the factors that has a large impact on the distribution of ventilation between dead space and gas exchanging alveoli is breathing pattern. Consider the patient in Case 1, when assessed he was noted to having rapid shallow breathing. His respiratory frequency was 40 per minute and his estimated VT was approximately 200 mL. As his VD/VT was 0.55, his VD would have been 200 · 0.55 = 110 mL. The subject’s VE was 40 · 0.2 = 8 L/minute, VD = 40. 0.11 = 4.4 L/minute, and VA = 8 − 4.4 = 3.6 L/minute. If VE were to remain the same (8 L/minute) and his breathing pattern were to change to slower and deeper, for example f = 20 and VT = 400 mL. In this latter case VD would be 20 · 0.11 = 2.2 L/minute and compartment VA would be 8 − 2.2 = 5.8 L/minute. What impact will this have on his gas exchange? This is the topic of the next section.
VA and CO2
Relation between VA and PaCO2
During steady state conditions of ventilation and perfusion, the rate of CO2 production (VCO2), at the tissue level, is constant and equals the rate of CO2 elimination at the lung. Alveolar CO2 concentration is directly related to CO2 production (VCO2) and inversely related to CO2 elimination which is controlled by VA. This relationship is also derived using the laws of conservation of mass for carbon dioxide,2 :
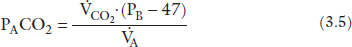
where PB is barometric pressure and 47 is water vapor pressure at 37°C.
Conventionally, PACO2 is expressed in mmHg, VA in L/minute at BTPS (Body Temperature Pressure Saturated) and VCO2 is expressed in mL/minute at STPD (Standard Temperature Pressure Dry). To account for PB, the difference in units between VA (L/minute) and VCO2 (mL/minute), and to standardize BTPS conditions with STPD one needs to multiply the right-hand side of the equation by a correction factor k (equals 0.863). Also, since CO2 is a very diffusible molecule across biologic membranes PaCO2 can be substituted for PACO2 and the equation can be written in the following form:

This equation expresses a very important core concept as it relates effective breathing (as represented by VA) to the metabolic rate of CO2 production (VCO2). Thus, the measurement of PaCO2 expresses whether VA is adequate for the metabolic needs of the body without measuring either VA or VCO2. If normally PaCO2 is 40 mmHg, then a doubling to 80 mmHg means that VA is only half of what is normally required for the body’s CO2 output. In other words, at a given metabolic rate, PaCO2 is inversely proportional to VA.
Going back to Case 1, at the end of the last section, we wondered what would happen to the patient’s gas exchange if he were to change his breathing pattern.
From Eq. (3.6), substituting 80 for PaCO2, 0.863 for k, and 3.6 for VA, gives a VCO2 of 333 mL/minute. Using the same equation, by changing VA from 3.6 to 5.8 L/minute, and assuming that VCO2
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


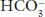 of 24 mEq/L will be abnormal at a
of 24 mEq/L will be abnormal at a 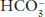 of 15 mEq/L.
of 15 mEq/L.