Fig. 11.1
Compartmental model for propofol using the Eleveld PK model for a 70-kg, 35-year-old male patient
The three compartments in the above PK model represent the volumes for the initial or central drug distribution volume (V1), the intermediate or fast-peripheral drug distribution (V2), and the slow-peripheral drug distribution (V3). When an intravenous dose of propofol is administered, it is assumed to be immediately and completely distributed throughout the central compartment volume. This is of course not true; however, for the vast majority of applications of the PK model, this captures the behavior of drug administration to a satisfactory degree. When drug appears in the central compartment, it immediately begins transporting to the fast-peripheral and slow-peripheral compartments, as well as being eliminated from the body (or otherwise rendered inactive). The rates of drug transport are represented by Q2, Q3, and CL, respectively. The distinction between V2 and V3 as fast or slow is essentially arbitrary; V2 is taken to represent the compartment with the faster equilibration time compared to V3. Sometimes a total volume of distribution parameter is described, Vss, which is the sum of V1, V2, and V3. The behavior of the three-compartment model can be fully described by a set of linear differential equations. For the standard three-compartment PK model, these are:
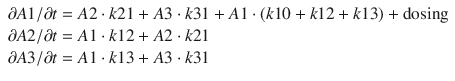 where
where 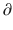 A1/
A1/ 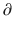 t represents the derivative of A1, the amount of drug in the central compartment, with respect to time, i.e., the rate of change in A1. Likewise
t represents the derivative of A1, the amount of drug in the central compartment, with respect to time, i.e., the rate of change in A1. Likewise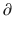 A2/
A2/ 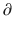 t and
t and 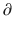 A3/
A3/ 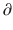 t represent the derivatives of drug amounts in the fast- and slow-peripheral compartments, respectively. The values for A1, A2, and A3 represent the amount of drug accumulated in the central, fast-peripheral, and slow-peripheral compartments, respectively. The predicted concentration of drug in a compartment is the amount of the drug divided by the corresponding volume; thus, the predicted concentration in the central compartment is A1/V1. Usually for propofol, before initial dosing, these variables are assumed zero. In contrast, for endogenous compounds, the amounts in the compartments may have some steady-state values. Intravenous drug dosing is applied to the central compartment, and thus following a bolus dose, the amount of drug in the central compartment, A1, is stepwise increased at the moment of dosing. For a continuous infusion, the derivative of the amount of drug in the central compartment is increased by the rate of continuous infusion per unit time. The rate constant k10 represents the rate of drug transport out of the body (or otherwise rendered inactive), and k21, k12, k31, and k13 represent the rate of drug transport between the peripheral compartments and the central compartment. Calculation of these rate constants from more meaningful compartmental volumes and clearances is:
t represent the derivatives of drug amounts in the fast- and slow-peripheral compartments, respectively. The values for A1, A2, and A3 represent the amount of drug accumulated in the central, fast-peripheral, and slow-peripheral compartments, respectively. The predicted concentration of drug in a compartment is the amount of the drug divided by the corresponding volume; thus, the predicted concentration in the central compartment is A1/V1. Usually for propofol, before initial dosing, these variables are assumed zero. In contrast, for endogenous compounds, the amounts in the compartments may have some steady-state values. Intravenous drug dosing is applied to the central compartment, and thus following a bolus dose, the amount of drug in the central compartment, A1, is stepwise increased at the moment of dosing. For a continuous infusion, the derivative of the amount of drug in the central compartment is increased by the rate of continuous infusion per unit time. The rate constant k10 represents the rate of drug transport out of the body (or otherwise rendered inactive), and k21, k12, k31, and k13 represent the rate of drug transport between the peripheral compartments and the central compartment. Calculation of these rate constants from more meaningful compartmental volumes and clearances is:
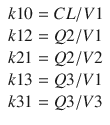 The differential equations can be used to obtain a predicted time course of drug distribution and elimination by finding an approximate solution using an ordinary-differential-equation (ODE) solver algorithm. If the infusion profile consists of simple bolus administrations or as continuous infusions of fixed rate and duration, then analytical solutions are available for three-compartment models which can predict drug distribution profiles directly from the model compartmental characteristics using the model parameters and the timing and amounts of the bolus doses and continuous infusions. The analytical solutions have the benefit of being exact and not requiring approximation. These analytical solutions can also be used to find approximate solutions for more complex infusion profiles. The arbitrary infusion profile can be approximated by a summation of bolus doses and continuous infusions, and then the superposition principle of linear systems is applied using the results of the separate individual components of the infusion profile. When these are summed, they predict the time course of drug distribution from the more complex infusion profile. While this can be computationally complex for complex dosing profiles, in many realistic cases, it is considerably more efficient than using an ODE solver.
The differential equations can be used to obtain a predicted time course of drug distribution and elimination by finding an approximate solution using an ordinary-differential-equation (ODE) solver algorithm. If the infusion profile consists of simple bolus administrations or as continuous infusions of fixed rate and duration, then analytical solutions are available for three-compartment models which can predict drug distribution profiles directly from the model compartmental characteristics using the model parameters and the timing and amounts of the bolus doses and continuous infusions. The analytical solutions have the benefit of being exact and not requiring approximation. These analytical solutions can also be used to find approximate solutions for more complex infusion profiles. The arbitrary infusion profile can be approximated by a summation of bolus doses and continuous infusions, and then the superposition principle of linear systems is applied using the results of the separate individual components of the infusion profile. When these are summed, they predict the time course of drug distribution from the more complex infusion profile. While this can be computationally complex for complex dosing profiles, in many realistic cases, it is considerably more efficient than using an ODE solver.
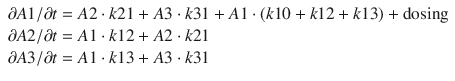
 A1/
A1/  t represents the derivative of A1, the amount of drug in the central compartment, with respect to time, i.e., the rate of change in A1. Likewise
t represents the derivative of A1, the amount of drug in the central compartment, with respect to time, i.e., the rate of change in A1. Likewise A2/
A2/ 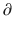 t and
t and 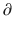 A3/
A3/ 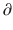 t represent the derivatives of drug amounts in the fast- and slow-peripheral compartments, respectively. The values for A1, A2, and A3 represent the amount of drug accumulated in the central, fast-peripheral, and slow-peripheral compartments, respectively. The predicted concentration of drug in a compartment is the amount of the drug divided by the corresponding volume; thus, the predicted concentration in the central compartment is A1/V1. Usually for propofol, before initial dosing, these variables are assumed zero. In contrast, for endogenous compounds, the amounts in the compartments may have some steady-state values. Intravenous drug dosing is applied to the central compartment, and thus following a bolus dose, the amount of drug in the central compartment, A1, is stepwise increased at the moment of dosing. For a continuous infusion, the derivative of the amount of drug in the central compartment is increased by the rate of continuous infusion per unit time. The rate constant k10 represents the rate of drug transport out of the body (or otherwise rendered inactive), and k21, k12, k31, and k13 represent the rate of drug transport between the peripheral compartments and the central compartment. Calculation of these rate constants from more meaningful compartmental volumes and clearances is:
t represent the derivatives of drug amounts in the fast- and slow-peripheral compartments, respectively. The values for A1, A2, and A3 represent the amount of drug accumulated in the central, fast-peripheral, and slow-peripheral compartments, respectively. The predicted concentration of drug in a compartment is the amount of the drug divided by the corresponding volume; thus, the predicted concentration in the central compartment is A1/V1. Usually for propofol, before initial dosing, these variables are assumed zero. In contrast, for endogenous compounds, the amounts in the compartments may have some steady-state values. Intravenous drug dosing is applied to the central compartment, and thus following a bolus dose, the amount of drug in the central compartment, A1, is stepwise increased at the moment of dosing. For a continuous infusion, the derivative of the amount of drug in the central compartment is increased by the rate of continuous infusion per unit time. The rate constant k10 represents the rate of drug transport out of the body (or otherwise rendered inactive), and k21, k12, k31, and k13 represent the rate of drug transport between the peripheral compartments and the central compartment. Calculation of these rate constants from more meaningful compartmental volumes and clearances is: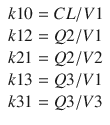
Sigmoidal E max Pharmacodynamic Models
While the PK of propofol receives considerable attention in modern anesthetic medicine and research, it is in reality a secondary issue. Drugs are primarily administered to achieve some desired drug effect. It is the desired drug PD effect which determines rational drug therapy, not the time course of drug concentrations in the body needed to achieve the desired effect. While the PK of anesthetic is indeed important to understand and consider, it is not the raison d’être of anesthetic drug dosing. For propofol, in nearly all cases, this is some degree of anesthesia or sedation.
Propofol central compartment concentrations show considerable hysteresis with the majority of PD effects, and thus a theoretical effect compartment is often used to introduce a delay between propofol central compartment concentrations and the PD effects. This “collapses” the hysteresis loop and establishes a fixed relationship between a hypothetical effect-site concentration and the concordant EEG effects. In addition, there are often upper and lower limits for PD effects, and there may only be a limited range of propofol concentrations between which the drug effect varies between these limits. Thus, for the majority of PD effects of propofol, a sigmoidal E max model is used where the effect-site concentrations follow the central compartment concentration by a first-order time constant, typically referred to as k e0. The differential equations for the effect compartment are:
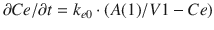 where A(1) and V1 maintain the same meaning as in the PK differential equations as the amount of propofol in the central compartment and the volume of the central compartment. The equation
where A(1) and V1 maintain the same meaning as in the PK differential equations as the amount of propofol in the central compartment and the volume of the central compartment. The equation 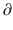 Ce/
Ce/ 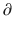 t represents the rate of change in concentration of propofol in a hypothetical effect compartment over time. Note that the differential equations do not consider the amount or mass of drug transfer between the central and effect compartments. The amount is assumed small enough to be negligible . This approach allows the PK model estimation to be performed separately from the PD model estimation.
t represents the rate of change in concentration of propofol in a hypothetical effect compartment over time. Note that the differential equations do not consider the amount or mass of drug transfer between the central and effect compartments. The amount is assumed small enough to be negligible . This approach allows the PK model estimation to be performed separately from the PD model estimation.
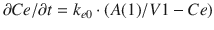
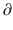 Ce/
Ce/ 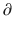 t represents the rate of change in concentration of propofol in a hypothetical effect compartment over time. Note that the differential equations do not consider the amount or mass of drug transfer between the central and effect compartments. The amount is assumed small enough to be negligible . This approach allows the PK model estimation to be performed separately from the PD model estimation.
t represents the rate of change in concentration of propofol in a hypothetical effect compartment over time. Note that the differential equations do not consider the amount or mass of drug transfer between the central and effect compartments. The amount is assumed small enough to be negligible . This approach allows the PK model estimation to be performed separately from the PD model estimation.The equation for transforming the predicted propofol effect-site concentration to a scaled drug effect is:
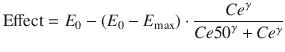 where Ce represents the predicted effect-site concentration at some time point, E 0 is the drug effect in the absence of propofol, E max is the theoretical maximal drug effect in the presence of arbitrarily high concentrations of propofol, Ce50 represents the predicted effect-site concentration when drug effect is halfway between E 0 and E max, and γ describes the steepness of the relationship between effect-site concentration and drug effect.
where Ce represents the predicted effect-site concentration at some time point, E 0 is the drug effect in the absence of propofol, E max is the theoretical maximal drug effect in the presence of arbitrarily high concentrations of propofol, Ce50 represents the predicted effect-site concentration when drug effect is halfway between E 0 and E max, and γ describes the steepness of the relationship between effect-site concentration and drug effect.
Interindividual Variability
While Fig. 11.1 shows the compartmental volumes and clearances for a particular population typical individual, all of the PK parameters show considerable interindividual variability. This is expressed as variability in model parameters across individuals but manifests itself as a variability in time course of drug concentrations for a given drug administration regimen. To provide an impression of the degree of variability of propofol distribution and elimination, Fig. 11.2 shows the time course for 100 hypothetical individuals, all of which are 70-kg, 35-year-old male patients, but who have randomly generated PK parameters, based on the variability of the different PK parameters in real datasets. The left panel shows the time course of propofol central compartment concentration following a bolus dose of 2 mg/kg. The right panel shows the propofol central compartment concentration for an infusion of 0.2 mg/kg/min for a duration of 30 min. This figure gives the reader an impression of the degree of variability across the population.
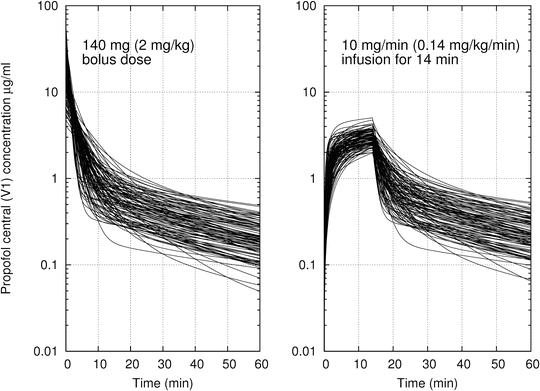

Fig. 11.2
The time course of propofol central compartment concentration for 100 simulated individuals who are 70-kg, 35-year-old male patients. Model parameters calculated using the Eleveld PK model
A Short History of Compartmental PK-PD Models for Propofol
A considerable number of PK models for propofol can be found in the literature. For the most part, these have been focused on some specific subpopulation such as children, adults, or the obese. More recently, PK models have been published which attempt to provide unified models for multiple subpopulations. An exhaustive historical review would be too lengthy for this chapter, so we will focus on a selection of the models which are particularly relevant to the scientific progress of propofol PK models and TCI applications.
One of the first investigations of the PK of Diprivan appeared in the literature in 1985 and was performed by Kay [6] who obtained propofol concentration data from 12 patients and estimated a three-compartment PK model to capture the distribution and elimination characteristics. The estimated CL was about 1.8 l/min, and the volume of distribution was quite large, about 755 l. This verified the idea that the very high lipid solubility of propofol would lead to large a volume of distribution.
The first important development toward the possibility of administration of propofol using target-controlled infusion (TCI) was the development of the Diprifusor TCI system. This system was based on PK parameters proposed by Gepts [7] and later modified by Marsh in 1991 (the Marsh parameters were published in passing in an article on the performance of an adapted model in children) [8]. The TCI system allows drug infusion profiles to be calculated which would achieve some desired concentration profile in a population typical individual. When applied to an individual selected from a population, the exact desired concentration profile would not be exactly replicated. However, the approach does enable TCI system users to modulate anesthetic depth with greater ease and accuracy compared to the more straightforward direct determination and manual implementation of infusion rates. Although the equations of the Diprifusor PK model are typically presented as rate constants, here they are presented as volumes and clearances referenced to 70 kg:
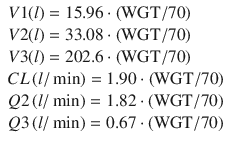 In 1994, the Kataria PK model [8] was published. It focused not only on the development of a PK model for propofol for children but also on some appropriate numerical methods for PK model estimation and evaluating PK model predictive performance. The focus was on comparing the performance of PK models developed from a population approach and those developed using a naive-pooled approach. The conclusion was that, although the naive-pooled approach may provide good model fits to data, the resulting model is not optimal for predictions under conditions differing from the experiment itself. Thus, predictions from a population PK model are expected to be superior than those developed using a naive-pooled approach. The equations for the Kataria PK model are:
In 1994, the Kataria PK model [8] was published. It focused not only on the development of a PK model for propofol for children but also on some appropriate numerical methods for PK model estimation and evaluating PK model predictive performance. The focus was on comparing the performance of PK models developed from a population approach and those developed using a naive-pooled approach. The conclusion was that, although the naive-pooled approach may provide good model fits to data, the resulting model is not optimal for predictions under conditions differing from the experiment itself. Thus, predictions from a population PK model are expected to be superior than those developed using a naive-pooled approach. The equations for the Kataria PK model are:
 where WGT is the individual’s weight in kg and AGE is the individual’s age in years. Note that the Kataria model parameters do not have good extrapolation properties. A 12-kg, 2-year-old child is predicted to have a V2 less than zero. As such the slope of the age relationship is likely overestimated.
where WGT is the individual’s weight in kg and AGE is the individual’s age in years. Note that the Kataria model parameters do not have good extrapolation properties. A 12-kg, 2-year-old child is predicted to have a V2 less than zero. As such the slope of the age relationship is likely overestimated.
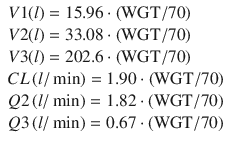

In 1998 Schnider published a PK model [9] intended to investigate the influence of methods of administration—bolus versus continuous infusions—on the estimated PK parameters. Patient covariates such as lean body mass and weight were found to play a role in parameter scaling for some, but not all parameters. A year later Schnider followed up the PK model with the corresponding PD analysis [10] which found an influence of age on both the k e0 (plasma-effect-site equilibration rate constant) and the steady-state sensitivity EC50 of individuals to propofol. The PD measure was the CUP (canonical univariate parameter) which is an encephalographic (EEG) measure intended to describe drug effect (hypnosis). For the same dose, older individuals were found to be more sensitive than younger individuals but achieved these drug effects more slowly than younger individuals. The Schnider model has found considerable success as a PK-PD model for TCI applications and is programmed into a number of commercially available infusion pumps. The equations for the Schnider PK and models are:


where HGT is the individual’s height in cm, AGE is the individual’s age in years, and LBM is the individual’s estimated lean body mass. Schnider used the James equation [11] to estimate LBM as follows:
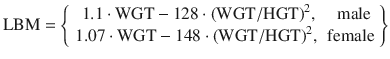 When applied to large, obese individuals, the Schnider model exhibits paradoxical behavior, predicting very small values for lean body mass (LBM) for very large individuals [12]. This is a result of the quadratic form of the James equation, having a convex parabolic shape. Some commercial applications of the Schnider PK-PD model avoid the paradoxical behavior by refusing to accept some ranges of patient weights as inputs.
When applied to large, obese individuals, the Schnider model exhibits paradoxical behavior, predicting very small values for lean body mass (LBM) for very large individuals [12]. This is a result of the quadratic form of the James equation, having a convex parabolic shape. Some commercial applications of the Schnider PK-PD model avoid the paradoxical behavior by refusing to accept some ranges of patient weights as inputs.
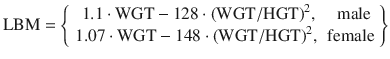
In 2000, Schuttler published a large multicenter PK analysis [13] by using data from seven different datasets from five different research groups. This was the first attempt to produce a unified PK model for both children and adult populations. It was the largest PK analysis to date by a considerable margin involving 4112 propofol concentrations from 270 individuals over a wide age range of 3–88 years. The final model used total body weight, age, method of administration (bolus vs. infusion), and sampling site (arterial vs. venous sampling) as covariates. The final model showed that PK model compartmental volumes and clearances (with the exception of V3) could be scaled to normalized total body weight to power exponents between 0.55 and 0.75. The equations of the Schuttler model are:
![$$ \begin{array}{l}V1(l)=9.3\cdot {\left(\mathrm{W}\mathrm{G}\mathrm{T}/70\right)}^{0.71}\cdot {\left(\mathrm{AGE}/30\right)}^{-0.39}\cdot \left\{\begin{array}{cc}\hfill 1,\hfill & \hfill \mathrm{infusion}\hfill \\ {}\hfill 2.61,\hfill & \hfill \mathrm{bolus}\hfill \end{array}\right\}\\ {}V2(l)=44.2\cdot {\left(\mathrm{W}\mathrm{G}\mathrm{T}/70\right)}^{0.61}\cdot \left\{\begin{array}{cc}\hfill 1,\hfill & \hfill \mathrm{infusion}\hfill \\ {}\hfill 1.73,\hfill & \hfill \mathrm{bolus}\hfill \end{array}\right\}\\ {}V3(l)=266\\ {}CL\left(l/ \min \right)=1.44\cdot {\left(\mathrm{W}\mathrm{G}\mathrm{T}/70\right)}^{0.75}-\left\{\begin{array}{cc}\hfill 0,\hfill & \hfill \mathrm{AGE}\ \le 60\hfill \\ {}\hfill 0.045\cdot \left(\mathrm{AGE}-60\right),\hfill & \hfill \mathrm{AGE} > 60\hfill \end{array}\right\}\\ {}Q2\left(l/ \min \right)=2.25\cdot {\left(\mathrm{W}\mathrm{G}\mathrm{T}/70\right)}^{0.62}\cdot \left\{\begin{array}{cc}\hfill 1,\hfill & \hfill \mathrm{arterial}\hfill \\ {}\hfill 0.6,\hfill & \hfill \mathrm{venous}\hfill \end{array}\right\}\cdot \left\{\begin{array}{cc}\hfill 1,\hfill & \hfill \mathrm{infusion}\hfill \\ {}\hfill 3.02,\hfill & \hfill \mathrm{bolus}\hfill \end{array}\right\}\\ {}Q3\left(l/ \min \right)=0.92\cdot {\left(\mathrm{W}\mathrm{G}\mathrm{T}/70\right)}^{0.55}\cdot \left\{\begin{array}{cc}\hfill 1,\hfill & \hfill \mathrm{infusion}\hfill \\ {}\hfill 0.52,\hfill & \hfill \mathrm{bolus}\hfill \end{array}\right\}\end{array} $$
” src=”/wp-content/uploads/2017/07/A339434_1_En_11_Chapter_Equi.gif”></DIV></DIV></DIV></DIV><br />
<DIV class=Para>Despite being the most well-supported PK model at the time, it did not find widespread clinical application. A possible reason for the lack of acceptance is that the <SPAN id=ITerm36>Schuttler PK model </SPAN><SPAN id=ITerm37></SPAN>proposes different values for <SPAN class=EmphasisTypeItalic>V1</SPAN>, <SPAN class=EmphasisTypeItalic>V2</SPAN>, <SPAN class=EmphasisTypeItalic>Q2</SPAN>, and <SPAN class=EmphasisTypeItalic>Q3</SPAN> depending on the method of administration, bolus, or continuous infusions. In clinical applications, drug doses are often in the form of both boluses and continuous infusions. Those considering the applying of the Schuttler model for clinical application may be uncertain which of the predicted parameter values should be used for a proposed drug infusion regimen containing both boluses and continuous infusions. In reality, this is not an insurmountable technical problem if separate compartmental state variables can be maintained, one for each method of administration. The principle of superposition, a property of all linear systems, allows the predicted concentrations for the separate state variables to be additively combined. This is possible because the PK for an individual is linear with respect to dose and drug concentrations. Unfortunately, the superposition principle does not help solve the problem of whether the rate of infusion is an important criterion for discerning whether some drug administration should be considered a bolus or an infusion. Overall, perhaps the additional numerical complexity of this approach and the uncertainty of the precise distinction between a bolus dose and a continuous infusion were a barrier to more widespread application of the <SPAN id=ITerm38>Schuttler PK model </SPAN>compared to other PK models.</DIV><br />
<DIV id=Par18 class=Para>In 2001 and 2003, the <SPAN id=ITerm39>Paedfusor PK model </SPAN>was investigated in two studies [<CITE><A href=]() 14, 15] although the specific PK parameter set used was only published in 2005 in a separate publication [16]. The notable aspect of this model was nonlinear scaling of k10, which was scaled to weight to a power exponent of −0.3. This corresponds to a scaling of CL to a power exponent of 0.7 to total body weight. This is interestingly close to the power exponent of 0.75 found by Schuttler. This same power exponent of 0.75 is predicted by allometric scaling theory which has been supported by subsequently developed PK models. The Paedfusor PK model has been programmed into in commercially available TCI infusion pumps. The equations of the Paedfusor model were published as rate constants and unwieldy to express as volumes and clearances. The equations of the Paedfusor model are:
14, 15] although the specific PK parameter set used was only published in 2005 in a separate publication [16]. The notable aspect of this model was nonlinear scaling of k10, which was scaled to weight to a power exponent of −0.3. This corresponds to a scaling of CL to a power exponent of 0.7 to total body weight. This is interestingly close to the power exponent of 0.75 found by Schuttler. This same power exponent of 0.75 is predicted by allometric scaling theory which has been supported by subsequently developed PK models. The Paedfusor PK model has been programmed into in commercially available TCI infusion pumps. The equations of the Paedfusor model were published as rate constants and unwieldy to express as volumes and clearances. The equations of the Paedfusor model are:
 In 2005, Knibbe et al. published an interspecies two-compartment PK model [17] using data from rats, children, and adults. This impressive feat was made possible with the use of allometric scaling, a mathematical technique to scale models for body size. While allometric scaling has been a topic of interest in the biological sciences, it only came to the forefront in PK modeling in propofol in 1999 in a publication in the pediatric anesthesia sciences [18]. Allometric scaling has since found widespread application in PK models, especially those concerning patient groups with a wide range of sizes. The equations for the Knibbe PK model are:
In 2005, Knibbe et al. published an interspecies two-compartment PK model [17] using data from rats, children, and adults. This impressive feat was made possible with the use of allometric scaling, a mathematical technique to scale models for body size. While allometric scaling has been a topic of interest in the biological sciences, it only came to the forefront in PK modeling in propofol in 1999 in a publication in the pediatric anesthesia sciences [18]. Allometric scaling has since found widespread application in PK models, especially those concerning patient groups with a wide range of sizes. The equations for the Knibbe PK model are:
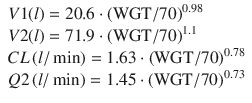 Also in 2005, Upton published a physiologically based PK model [19] which utilized considerable physiological information as model structural elements. The model structure was rather complex and required a considerable number of assumptions to make the model estimable from PK observations while avoiding issues of numerical stability and identifiability. Because of the complexity of the model equations, we do not repeat them here.
Also in 2005, Upton published a physiologically based PK model [19] which utilized considerable physiological information as model structural elements. The model structure was rather complex and required a considerable number of assumptions to make the model estimable from PK observations while avoiding issues of numerical stability and identifiability. Because of the complexity of the model equations, we do not repeat them here.





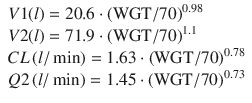
In 2010 Cortínez published a PK model [20] targeted to obese and lean individuals, applying concepts from allometric scaling to data collected from three different studies. They investigated whether other methods of parameter scaling such as linear scaling and the application of fat-free-mass (FFM) concepts could lead to an improved model but found that scaling the PK model parameters to total body weight using the theoretical allometric scaling power exponents provided the best model. The equations of the Cortínez PK model are:
 Currently, the most well-supported PK model for propofol is the general purpose PK model published by Eleveld [5] in 2014. This model was based on propofol data from several studies publicly available via the Open TCI website (http://www.opentci.org/) as well as other studies. The analyzed data contains 10,927 drug concentration observations from 660 individuals over an age range of 0.25–88 years and a weight range of 5.2–160 kg. The patient covariates used were weight, age, gender, and patient status (healthy volunteer vs. patient). The final model uses concepts from allometric scaling where volumes are assumed to scale linearly with normalized weight and clearances to the ¾ power exponent. Predictive performance of the model has been evaluated in the obese [21] and in cancer patients [22] and was found to be clinically acceptable. Further prospective evaluation of this model is needed to establish whether it can replace specialized PK models for children and adults and the obese. The equations of the Eleveld general purpose PK model for propofol are:
Currently, the most well-supported PK model for propofol is the general purpose PK model published by Eleveld [5] in 2014. This model was based on propofol data from several studies publicly available via the Open TCI website (http://www.opentci.org/) as well as other studies. The analyzed data contains 10,927 drug concentration observations from 660 individuals over an age range of 0.25–88 years and a weight range of 5.2–160 kg. The patient covariates used were weight, age, gender, and patient status (healthy volunteer vs. patient). The final model uses concepts from allometric scaling where volumes are assumed to scale linearly with normalized weight and clearances to the ¾ power exponent. Predictive performance of the model has been evaluated in the obese [21] and in cancer patients [22] and was found to be clinically acceptable. Further prospective evaluation of this model is needed to establish whether it can replace specialized PK models for children and adults and the obese. The equations of the Eleveld general purpose PK model for propofol are:



Perspective
If one considers the development of propofol PK models in the literature over the years, it is interesting to note that the individual models have not changed significantly since the 1985 when Kay showed that the individual time course of propofol concentration could be characterized by a mammillary three-compartment PK model. More than 25 years later, the same basic model is still in use. It is an interesting coincidence to note the predicted rate of clearance established by Kay in 1985 was 1.8 l/min while the rate predicted in 2014 by Eleveld was 1.53 l/min for patients and 1.83 l/min for healthy volunteers. Over the course of almost 30 years, the estimate of propofol clearance for adults has hardly changed.
There has been a lack of widespread applications of individual models more complex than the three-compartment mammillary model. This suggests that the quality and quantity of the individual PK data gathered in these investigations are not sufficiently informative to construct more detailed models on an individual level. This should put some perspective on efforts to develop PK models with a better connection to physiology, i.e., models with more detailed representation of physiological process as structures. If this approach is to become viable, PK modeling studies would likely need significantly more detailed and diverse kinds of observations than the 5–25 PK samples combined with on the order of ten covariate observations per individual.
What has changed significantly over the years is the breadth of demographic groups on which the PK models focus. The earliest models were targeted to healthy adult volunteers or adults undergoing some specific surgical intervention. Since 2005, these demographic groups have broadened significantly, and this has created more challenging conditions under which models can be developed and evaluated. The end result is improved models and more confidence in users that a chosen model is appropriate for some desired application. This broadening of demographic groups applied to propofol PK models has been the result of the application of allometric scaling.
Another aspect that has changed over the years is the choice a priori model structure. Earlier developed PK models tended to utilize (estimated) constants for parameter values in their a priori models. No covariates at all were assumed, not even weight. If the data was not very informative for those parameters, then hierarchical model building would not result in the addition of any covariates at all. For those parameters, the final model would simply be a constant value. While this approach can be numerically justified from the point of view of maintaining simplicity in the final structural model, the final models are less useful than they could be. Constant parameters are in general poor when good extrapolation properties are desired. One example of this is V1 in the Schnider model, which is a constant with no covariates at all. Extrapolation of the Schnider model to children is probably not sensible because it is very unlikely that children would have the same value for V1 as adults. If that were indeed true, then children and adults would require the same total dose amount (e.g., in mg) to achieve the same initial concentration. Anesthesiologists with clinical experience are likely to understand that children require smaller doses to achieve the same drug levels as an adult. If, on the other hand, Schnider had chosen a different a priori function for V1, then it is possible that the final model would have shown more reasonable extrapolation behavior and a smaller V1 for children than for adults. This model would then propose more reasonable initial doses and concentrations and thus likely be more useful for extrapolation. Most of the recently developed PK models incorporate allometric scaling in the a priori model. This approach has the positive property of ensuring more reasonable, but of course not necessarily perfect, extrapolation properties and making the final models more useful in general.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








