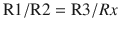Fig. 35.1
Clark-type oxygen electrode
When a voltage of 700 mV is applied across the electrodes the following reactions occur:
Cathode: O2 + 2H20 + 4e− = 4OH−
Electrolyte: KCl + OH− = KOH + Cl−
Anode: Ag + Cl− = AgCl + e−
The amount of electrons that are taken up at the cathode is proportional to the oxygen tension and this current can be processed and displayed as PO2.
The pH (Sanz) electrode works on the principle that an electrical potential develops across a glass membrane, which is proportional to the pH difference across it. The pH electrode consists of 2 “half” cells: a glass electrode and a reference electrode. The glass electrode is an Ag/AgCl electrode system enclosed in a glass membrane and maintaining a constant pH within itself, while the reference electrode is a Hg/HgCl electrode, which comes in contact with the blood sample through a semi-permeable membrane. The chloride solution acts as the bridge between the 2 electrodes. The whole system is maintained at 37 °C. Current flows from the reference electrode through the semi-permeable membrane through the sample in the measuring chamber and to the glass electrode. Depending on the pH of the sample, the potential will develop across the glass membrane, which will be displayed in pH units. The potential output is 60 mV per pH unit (◘ Fig. 35.2).
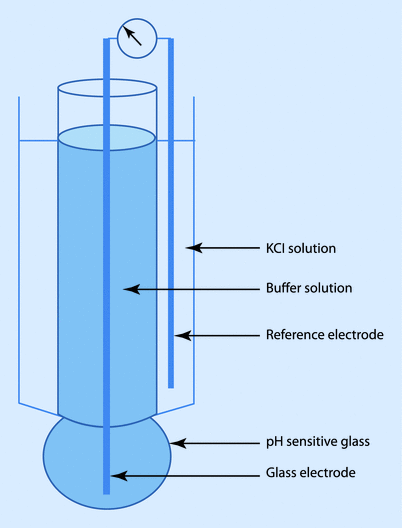

Fig. 35.2
pH (Sanz) electrode
The CO 2 (Severinghaus) electrode is similar to the pH electrode with the electrode in contact with a sodium bicarbonate solution and separated from the blood sample by a Teflon semipermeable membrane. CO2 from the blood sample diffuses across the membrane and reacts with the bicarbonate solution to form H+, which is measured by the pH electrode:
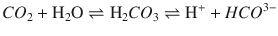
The amount of H+ produced is proportional to the PCO2 in the blood. Similar to the pH electrode, the whole system is maintained at 37 °C.
35.2.2 Hypothermia and Blood Gas
Solubility of all gases increases with a fall in temperature of the solvent and thus lowers its partial pressure. Therefore, hypothermia increases the solubility of O2 and CO2, and consequently lowers the PO2 and PCO2. The PCO2 decreases by approximately 2 mmHg and PO2 decreases by approximately 5 mmHg per °C below 37 C. Hypothermia also changes the pH; for every °C drop in temperature the pH increases by 0.015 units.
Since, the analysis of the blood sample occurs at 37 °C, in a hypothermic patient the PO2 and PCO2 values would be artificially high. The result can be corrected for the patient’s temperature. This becomes especially important in significantly hypothermic patients, such as during cold cardiopulmonary bypass or deep hypothermic circulatory arrest.
pH-STAT
Historically, it was thought that in a hypothermic patient undergoing cardiopulmonary bypass, a reduced PCO2 would result in cerebral vasoconstriction and ischemia. Therefore, CO2 was added to the oxygenator to maintain a temperature-corrected PCO2 of 40 mmHg (5.3 kPA) and a pH of 7.4. The advantage of this was increased cerebral blood flow allowing better oxygen delivery. However, there was concern that it could lead to micro-embolization and loss of autoregulation.
α(Alpha)-STAT
Hypothermia reduces the efficacy of the bicarbonate and the phosphate buffers and the amino acids (alpha imidazole ring of histidine) become the primary buffer. During hypothermia, pH increases because of low H+ (decreased dissociation), but electro-neutrality is maintained as there is less available OH−. This is more physiological. The advantages are maintenance of cerebral autoregulation and normal cellular transmembrane electro-neutrality. The resultant alkalosis better preserves protein function and enzyme activity. Therefore, proponents of α(alpha)-stat maintain uncorrected PCO2 and pH at normal levels. The α(alpha)-stat method is the more acceptable and standard approach.
35.3 Respiratory and Anesthetic Gas Measurement
35.3.1 Paramagnetic Oxygen Analyzer
Oxygen, because of its unpaired electron in the outer orbit, is “paramagnetic” or attracted toward a magnetic field, while most other gases used in anesthesia are “diamagnetic” or repel from a magnetic field. Historically, 2 spheres, connected together to look like a dumb-bell, filled with nitrogen (a diamagnetic gas) were suspended in a magnetic field. In the resting stage the dumb-bell would try to move away from the magnetic field. However, when oxygen-containing gas was passed around it, the oxygen being attracted to the magnetic field would move the dumb-bell toward the magnetic field, depending on the concentration of oxygen. This movement could be electronically extrapolated as the concentration of oxygen. However, the construction of modern analyzers has fewer moving parts, but still uses the same principle (◘ Fig. 35.3). A highly sensitive pressure transducer measures the pressure difference between 2 streams of gas: the “sample” and the “reference.” Further downstream to the transducer, both the gases pass through a common channel, across which a “pulsed” electromagnetic field is generated at around 100 Hz. When the magnetic field is applied, oxygen molecules are attracted toward it, causing a low pressure upstream. The pressure difference between the 2 streams, which is measured by the transducer, would be proportional to the difference in oxygen concentration. The electric output from the transducer displays it as volume percentage of oxygen in the sample gas. Of all the gases the anesthesiologists encounter, nitric oxide is the only other gas that is also paramagnetic.
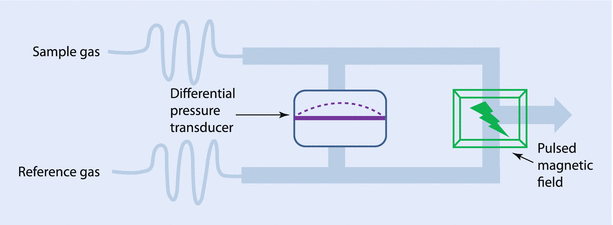

Fig. 35.3
Pulsed-field paramagnetic oxygen analyzer
35.3.2 Fuel Cell (Galvanic Cell)
The fuel cell is similar to the Clark polarographic electrode except that it generates its own voltage without any external power source. It consists of a gold cathode and a lead anode immersed in potassium hydroxide solution. Oxygen from the gas sample is reduced at the cathode to form OH-, which moves to the anode to form electrons, thus generating a potential difference. The current generated is proportional to the concentration of oxygen in the sample:
Cathode: O2 + 2H2O + 4e− → 4 OH−
Anode: 2Pb + 4(OH−) → 2PbO + 2H2O + 4e−
35.3.3 Infrared Spectrophotometry
Absorption spectroscopy is the fundamental principle used in capnography, pulse oximeter, and most anesthetics gas monitors. Molecules with 2 or more dissimilar atoms absorb infrared (IR) radiation and different molecules have distinct IR absorption spectra. The absorbance peak of CO2 and N2O are between 4 and 5 μm and that of the anesthetic gases are between 8 and 13 μm. According to the Beer-Lambert law, the amount of IR radiation absorbed is directly proportional to the concentration of the molecule and the distance travelled in the medium.
In a gas analyzer, a source emits IR radiation, which is passed through a chamber containing the sample gas and also a reference chamber and focused on an IR photo sensor. The amount of absorbed radiation is proportional to the concentration of the gas. Numerous readings per minute provide a continuous waveform of gas concentration during the respiratory cycle. There are 2 types of IR technology available today: (1) the “Blackbody Radiation,” which produces a broad spectrum and filter is used to obtain specific wavelengths of radiation; and (2) the “Microstream,” which generates IR emissions at specific wavelength that matches the absorption spectrum of the gas to be monitored.
Limitations of Infrared Spectroscopy
Oxygen, nitrogen, helium, xenon, and argon do not absorb IR radiation and cannot be measured by this technique. The absorption spectra of CO2 and N2O overlap and presence of N2O broadens the CO2 absorption spectrum (collision broadening), leading to a falsely elevated value. Water vapor absorbs IR and can interfere with measurement of CO2 and anesthetic agents. Hydro-fluoro-alkanes, used as propellants in inhalers, have an absorption spectrum similar to halothane and can interfere with measurement of volatile agents.
35.3.4 Pulse Oximeter
The conventional pulse oximeter consists of 2 light-emitting diodes, a photocell detector, and a microprocessor with a visual display unit. The light-emitting diodes emit light at wavelengths of 660 nm (red) and 940 nm (infrared), since these give a better separation of absorbance. At 940 nm the light absorbance of oxy-hemoglobin is one-and-a-half times more than that of deoxy-hemoglobin, while at 660 nm the deoxy-hemoglobin absorbs 10 times as much as oxy-hemoglobin (◘ Fig. 35.4). At 805 nm, both the deoxy-hemoglobin and the oxy-hemoglobin absorb equally and this is called the “isobestic” point. The ratio (R) of absorbance at 660 and 940 nm bear a linear relationship to oxygen saturation. At high O2 saturations, this ratio is less than 1. At approximately 85% saturation this ratio is equal to 1. The values for R can be mathematically calculated down to saturations of 0%, but these are not accurate clinically.
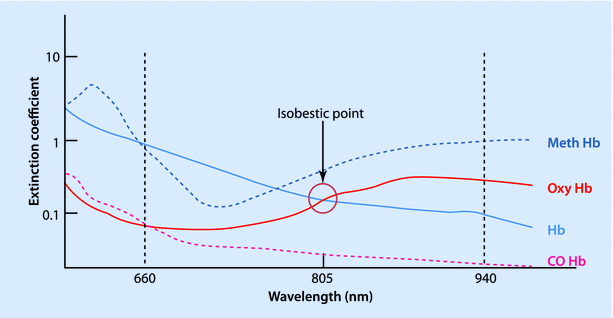

Fig. 35.4
Absorption spectrum of different forms of hemoglobin, according to wavelength of light
The main purpose of the pulse oximeter is to detect the amount of HbO in the arterial blood. However, at the fingertip, light is also absorbed by other tissue and venous blood. An ingenious concept is incorporated into modern pulse oximeters. With each pulse there is a surge of arterial blood across the measuring point and the amount of light absorbed would increase, cyclically. The pulse oximeter emits and analyzes light signals at a very rapid rate (400–600/s) and this can detect the peaks and troughs of the arterial pulse wave. If the light absorption at the trough (which includes all the tissue absorbers) is subtracted from the light absorption at the peak, then in theory the remaining is the absorption due to the added volume of arterial blood only. The ratio of the absorbance of the pulsatile to that of the non-pulsatile at both the wavelengths is calculated.
Even though traces of carboxyhemoglobin (COHb) and methemoglobin (MethHB) may be present normally, the pulse oximeter assumes the presence of only oxyhemoglobin and reduced hemoglobin. Significant levels of COHb or MethHB can causes error in pulse oximeter readings. Since the COHb absorbs the red light very similarly to HbO and does not absorb the infrared, the pulse oximeter tends to read higher values in presence of COHb. Methemoglobin absorbs both red and infrared waves equally and therefore the absorbance ratio, R, is 1. Therefore, the pulse oximeter tends to shift the SpO2 towards 85%. Other factors that interfere with the pulse oximetry reading are dark-colored nail polishes, dyes (methylene blue and indigo-cyanine green), high bilirubin levels, tremors or movement of the hand, vasoconstriction, and ambient light. If the signals from the finger are low, alternative sites—such as ear lobe, ala of the nostril, or, in neonates, the foot or the palm—could be used. Pulse oximeter probes used during magnetic resonance imaging (MRI) have a fiberoptic system as the wires in a standard probe would generate heat in the radio-frequency environment and can cause burns.
Co-oximeter
A Co-oximeter is a device that measures the blood concentration of carboxyhemoglobin (COHb), methemoglobin (MethHb), oxyhemoglobin (HbO2), and reduced hemoglobin (HHb) using a sample of the arterial blood. A non-invasive Co-oximeter (Masimo Rainbow® Pulse Co-oximeter; Masimo Corp., Irvine, CA), which looks similar to the usual pulse oximeter, is currently available. It uses multiple frequencies of light to calculate the saturation of carboxyhemoglobin, methemoglobin, oxyhemoglobin (SpO2), and total hemoglobin. It also measures the oxygen content (SpOC), the perfusion index, and the pleth variability index:5
Fractional Saturation: HbO/(Hb + HbO + MethHb + COHb) (needs a Co-oximeter)
Functional Saturation: HbO/(Hb + HbO) (pulse oximeter)
35.3.5 Mass Spectrometry
The concentration of a gas in a mixture can be measured by its mass-charge ratio. The sample of gas is passed through an ionizing chamber where an electron gun ionizes the molecules. These charged molecules are then accelerated through a magnetic field before striking a detector plate. The charged gas molecules are deflected by the magnetic field depending on their mass, and create a series of peaks on the detector plate. The position of these peaks identifies the gas and their height corresponds to the concentration. The mass spectrometer is very accurate but tedious and expensive, and is mainly used for research or monitoring gas samples from numerous operating rooms. The gas sample cannot be returned to the patient as the molecules are ionized.
35.3.6 Raman Scattering
When an electromagnetic radiation collides with a gas molecule, it normally scatters with the same energy, and this is known as Rayleigh scattering. This is how we see things even though they do not emit light of their own. However, occasionally collision of electromagnetic wave energizes the molecule and when it returns to its resting state, it emits the energy at a wavelength characteristic of the particular molecule. This is known as Raman scattering. This scattered light can be filtered out from the Rayleigh scattering and analyzed to identify the specific gas and its concentration. An intense beam of LASER is passed through a sample chamber and the Raman scattering is measured on a photodetector. This technique is fast and accurate and can be used to measure a number of gases. This technique is used to identify gases on distant planets.
35.3.7 Piezoelectric Absorption
Quartz crystal when placed in an electric field oscillates at a characteristic natural frequency. However, when such crystals are coated with oil, volatile anesthetic would dissolve in the lipid layer and increase the mass of the crystal, altering the frequency of oscillation. The change in frequency reflects the change in mass, which is proportional to the concentration of gas in the sample. The response time is fast, but it cannot differentiate between the gases.
35.4 Intra-arterial Blood Pressure Monitoring
The intra-arterial blood pressure (IABP) measurement system consists of a column of fluid connecting the arterial system to a pressure transducer. The arterial pressure wave transmits through the fluid column and vibrates the diaphragm of the transducer, which then converts it into an electrical signal.
35.4.1 Sine Wave
A wave is the movement of energy through a medium. Sine wave is the simplest waveform and can be considered as the path taken by a point around a circle and mathematically defined by function y = sin x. It is described by its “amplitude”—maximum displacement; and its “frequency”—number of cycles per second. Sine waves of differing amplitude and frequency can combine to form a complex wave. Conversely, a complex wave like the arterial pressure waveform can be broken down into multiple component waveforms. The arterial pressure wave would have a “fundamental” wave, with a frequency equal to the pulse rate (1–3 Hz) and a series of “harmonic” waves, with frequencies in multiples (up to 8–10 times) of the fundamental frequency (~24 Hz). The process of analyzing a complex wave into its constituent sine waves is known as Fourier analysis (◘ Fig. 35.5).
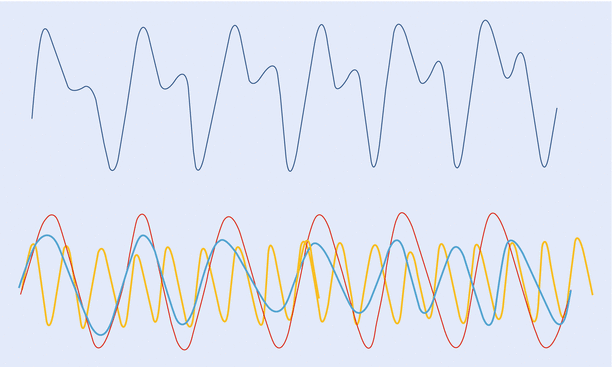

Fig. 35.5
A complex “arterial” waveform, which can be broken down into multiple, component sine waves (fundamental and harmonic). This analysis is known as Fourier analysis
35.4.2 Natural Frequency and Resonance
Every material when struck oscillates at its “natural” frequency and this depends on physical properties of the material, such as density and thickness and also of the adjacent material. If an external force or a waveform, with a frequency similar to the natural frequency, is applied, the material would oscillate at its maximal amplitude and this is known as “resonance.” Therefore, if the natural frequency of the IABP monitoring system is close to the frequency of any of the components of an arterial waveform, it would vibrate excessively and distort the signal. Since the range of pulse rate usually seen clinically is 60–180/min or 1–3 Hz, the natural frequency of the arterial pressure transducer should be greater than 8–10 times the fundamental frequency. Most commercially available systems have a natural frequency of around 200 Hz. However, the natural frequency of the system can be reduced by the addition of 3-way taps, long tubing, presence of air-bubbles and clots and it is increased by using shorter and wider arterial cannula and tubing.
35.4.3 Damping
The arterial pressure monitor, in addition to having a high natural frequency, also needs an appropriate damping coefficient (zeta or ζ). Damping can be construed as the force that brings the transducer system back to its resting stage after the oscillation in order to detect the next wave. Therefore a critical damping is essential for proper functioning of the system, and overdamping or underdamping would adversely affect the measurement. Underdamping leads to large amplitude oscillations and factitiously high systolic and low diastolic pressure readings, although the mean arterial pressure may be accurate. On the contrary, in an overdamped system, the oscillations are subdued and blunted and it reads an erroneously low systolic and a high diastolic pressure, while the mean pressure reading would remain unchanged. In an IABP measuring system, damping is increased by factors that impede fluid flow in the system, namely density of the fluid, a compliant tubing and narrowing (kinks, vasospasm) or obstruction (clots, air bubbles), which are very similar to the factors that lower the natural frequency. The optimal damping coefficient of 0.7 provides the balance between rapid response and accuracy.
35.4.4 “Fast Flush” Test
The IABP monitoring system uses a flushing system, wherein a bag of heparinized-saline, pressurized to 300 mmHg infuses at 2–4 ml/h through the fluid-filled tubing to maintain the patency of the cannula. This system can also be used to perform the “fast flush” test to calculate the natural frequency and the damping coefficient of the system. A short burst of flush is applied and the pressure waves on the monitor are analyzed. The square wave corresponds to the exposure of the transducer to the 300 mmHg pressure of the flushing system. This is followed by sharp waves oscillating at the natural frequency of the system and it can be calculated by dividing the screen speed by the wavelength of the resonant waves. Therefore, the closer the oscillation cycles, the higher the natural frequency. Similarly, the ratio of the amplitudes of the second to the first post-flush waves (amplitude ratio) can be used to derive the damping coefficient from standard nomograms. A low amplitude ratio corresponds to a high damping coefficient, or the system comes to rest quickly (◘ Fig. 35.6).
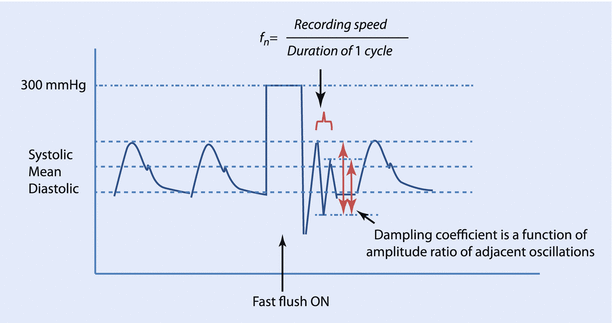

Fig. 35.6
Fast flush test
Clinical Significance
Although the desired technical requirements for arterial pressure monitoring are a natural frequency greater than 25 Hz and a damping coefficient of 0.7, these conditions are rarely met in routine clinical practice. Most catheter-tubing transducer systems are underdamped (damping coefficient of 0.15–0.45) and have an acceptable natural frequency of 12–25 Hz. If the fn of the system is less than 7 Hz, it is unacceptable and if the fn is greater than 24 Hz, damping will have minimal effect on the arterial wave recording.
35.4.5 Transducer
Transducers convert one form of energy into another and the pressure transducers used for IABP monitoring converts pressure into electrical signal that can be measured and displayed. The arterial pressure wave transmits down the fluid column and displaces the diaphragm of the transducer. This displacement is measured using a strain gauge, which is based on the physical principle that the resistance of a wire increases when it is stretched and decreases when compressed. Therefore, the pressure exerted by the arterial pulse wave on the diaphragm would compress and stretch the wire attached to the diaphragm and the change in resistance of the wire can be measured precisely by incorporating it as one of the limbs of a “Wheatstone bridge.”
Wheatstone Bridge
Wheatstone bridge is a circuit designed to measure an unknown resistance. Current is passed through 2 parallel circuits, each with 2 resistances in series. A galvanometer connects the 2 circuits in the middle to detect any flow of current between the circuits (◘ Fig. 35.7). The resistances can be adjusted so that no current flows through the galvanometer and the bridge is said to be balanced, and at this stage the ratio of the resistances is: