Physical Measurements in Anesthesia

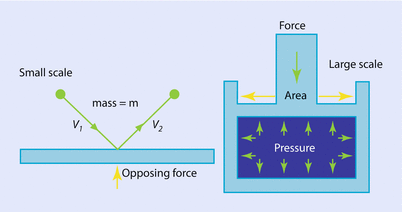
Fig. 33.1

Gravity will cause a 1 kg object to accelerate at a rate of 9.81 kg m⁻¹ s⁻²; therefore the force of gravity on a 1 kg object will be 9.81 N. This is referred to as a kilogram weight. One newton is therefore equal to 1/9.81 kg weight, which is 102 g weight.

Therefore the pressure of 1 Pa is equal to a force of 102 g m⁻². This is clearly a very small amount of pressure, so the unit of pressure commonly used is the kilopascal (kPa), not the pascal.

Discussions about physics in anesthesia may be confusing because of a variety of pressure units used in the clinical literature:

Atmospheres (atm)
bar
mmHg
cm H₂O
pascals (Pa)
PSI (pounds per square inch)
5 N/m²
dynes/cm²

In order for the reader to relate to these different units, atmospheric pressure at sea level may be written as:

$\begin{array}{l}1\ \mathrm{atm}=1.01\ \mathrm{bar}=760\ \mathrm{mm}\ \mathrm{Hg}=1,033\ \mathrm{cm}\ {\mathrm{H}}_2\mathrm{O}=101\ \mathrm{kPa}\\ {}=14.7\ \mathrm{PSI}=101,325\ \mathrm{N}/{\mathrm{m}}^2=1,013,250\ \mathrm{dynes}/{\mathrm{cm}}^2\end{array}$

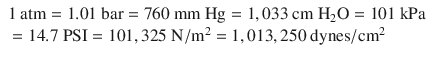
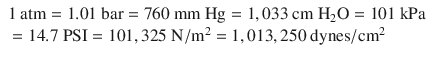
American engineers often use PSI units. Scientists often use Pascal units (SI). Clinicians often use mmHg for blood pressures and cm H₂O for airway pressures and positive end-expiratory pressure (PEEP) levels (and sometimes for central venous pressure reports).

33.1.2 Pressure Measurement

Historically, pressure has commonly been measured using a column of liquid. Your more venerable colleagues will be familiar with using a manometer tube to measure central venous pressure (CVP). This consisted of a flexible tube that was filled with saline before being attached to a central venous line. The other end was attached to the bottom of an open topped glass tube, again filled with saline. The glass tube or manometer had gradations of centimeters marked on the side and when the “0” was placed at the height of the heart, the CVP could be measured off the side of the manometer (◘ Fig. 33.2).

Fig. 33.2

A glass manometer

A similar mechanism may be used to measure higher pressures, and mercury would often be used for this range of pressure, as mercury is 13.6 times denser than water. It is easy to see that a 100 cm column of water could be represented by a 73.6 mm column of mercury—a much more manageable height. One atmosphere would be represented by 760 mm of mercury and this was put to good use in early barometers (◘ Fig. 33.3).

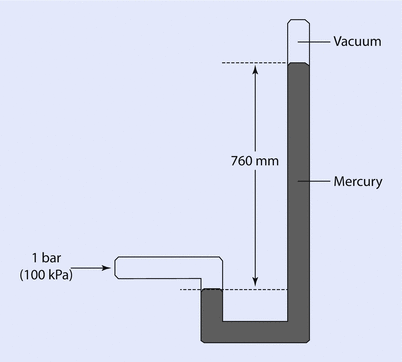
Fig. 33.3

An early barometer

An alternative to a column of fluid is the Bourdon gauge, which is an aneroid gauge (from the Greek a-neros meaning without liquid). This type of aneroid gauge is based on the principle of a metallic tube uncoiling when the internal pressure increases, which then moves a needle through a series of levers and gears (◘ Fig. 33.4).

Fig. 33.4

The internal construction of a bourdon tube gauge (dial and indicator needle removed). Note the curved brass tube that slightly straightens out with pressurization, eventually rotating the indicator needle (Source: Yegor Chernyshev at English Wikipedia. Image licensed under CC BY-SA 3.0 via Creative Commons)

A pressure measurement may be displayed in a number of ways and the following are all common within medicine and anesthesia:

Absolute pressure is “zero-referenced” with respect to a perfect vacuum, and thus is equal to gauge pressure plus atmospheric pressure.
Gauge pressure is “zero-referenced” with respect to ambient air pressure (atmospheric pressure), and thus is absolute pressure minus atmospheric pressure.
Differential pressure is the difference in pressure between 2 points.

For the most part, the anesthesiologist can disregard atmospheric pressure and therefore use gauge pressure readings that are relative to atmospheric pressure. Gas cylinder, blood pressure, and ventilator pressure readings are all gauge pressure readings.

To look at these readings in the clinical context, a full oxygen cylinder has a gauge pressure reading of 137 bar. Atmospheric pressure is approximately 1 bar, therefore the absolute pressure is the sum of gauge pressure and atmospheric pressure, equaling 138 bar.

33.1.3 Dalton’s Law of Partial Pressures

When a mixture of nonreacting, pure gases are placed in a sealed container, the pressure that each exerts on the walls of the container is proportional to the percentage that that gas makes of the whole mixture.

For example, if a cylinder of Entonox® (a medical gas mixture of 50% O₂ and 50% N₂O; manufactured by BOC Healthcare, Manchester, UK) is at a pressure of 100 kPa, the oxygen will exert a partial pressure of 50 kPa and the nitrous oxide also will exert a partial pressure of 50 kPa.

This is summarized by Dalton’s law of partial pressures which states that:

In a mixture of non-reacting gases, the total pressure exerted is equal to the sum of the partial pressures of the individual gases.

The formulaic representation of this law is:

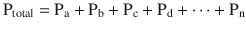
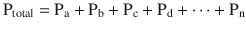
${\mathrm{P}}_{\mathrm{total}}={\mathrm{P}}_{\mathrm{a}}+{\mathrm{P}}_{\mathrm{b}}+{\mathrm{P}}_{\mathrm{c}}+{\mathrm{P}}_{\mathrm{d}}+\dots +{\mathrm{P}}_{\mathrm{n}}$

A good representation of this equation is to see how Dalton’s law of partial pressures applies to air (◘ Fig. 33.5).

Fig. 33.5

A representation of how Dalton’s law of partial pressures applies to air

33.1.4 Medical Gas Cylinders

Medical gases may be delivered in cylinders of various sizes (◘ Table 33.1) made of aluminum, stainless steel, or other nonreactive material. Medical grade oxygen is also commonly delivered as a liquid by tanker and stored in an insulated, pressurized container on the hospital site. All medical gases are produced by stringently licensed manufacturers ensuring 99.995% purity.

Table 33.1

Sizes of commonly used medical gas cylinders

Size	Capacity (L)	Pressure (psi)	Tare weight (kg)	Valve type
B	200	1900	2.27	Pin index
D	400	1900	3.4	Pin index
E	660	1900	5.4	Pin index
F	1360	1900	14.5	Bull nose
G	3400	1900	34.5	Bull nose
H	6900	2200	53.2	Bull nose
M	3450	2200	29.0	Bull nose

Although medical gas cylinders are made from strong materials, they should be handled with care as an explosion may not be prevented when dropped on a concrete floor. Cylinders should be stored upright, indoors, protected from the weather, and at a constant temperature. Manufacturers regularly examine and test cylinders resulting in faulty cylinders being withdrawn from service. An internal test of all cylinders is carried out periodically using an endoscope.

Color coding is used to identify the contents of gas cylinders; however, color coding varies throughout the world. An International Organization for Standardization (ISO) standard, ISO 32, covers colors of cylinders for medical gases but not all countries use this standard. In the United States, for example, color coding is not regulated by law. The common color codes for medical gas cylinders are displayed in ◘ Fig. 33.6.

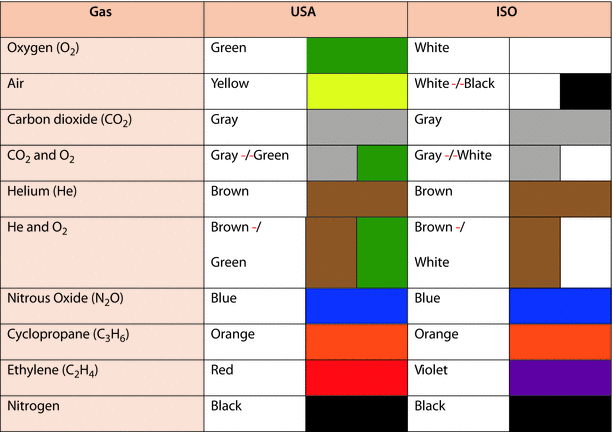
Fig. 33.6

Color coding of USA and ISO medical gases

On the top of the cylinder is an identification label giving details of contents, pressures, volumes, and any hazard warnings. Seated in the neck of the cylinder is the valve that closes the cylinder and ensures that the contents do not leak. This valve also allows a secure fit for refilling and for attachment to the yoke that may then deliver oxygen directly to the patient or to the anesthesia machine for delivery.

On the face of the cylinder valve is a series of small holes below the outlet for the gas (◘ Fig. 33.7, top left). These accept a reciprocal pin system, called the Pin Index Safety System (PISS), on the yoke (◘ Fig. 33.7, top right). The position of the holes and matching pins are specific to a particular gas cylinder, thereby helping to ensure that the correct gas is connected to the correct yoke.

Fig. 33.7

Top: Cylinder valve and receiving yoke showing pin index system. Bottom: Bull nose connection system used on larger cylinders

On larger cylinders a bull nose connection system is used (◘ Fig. 33.7, bottom left and right) with a variety of male and female connections as well as right and left hand threads in order to reduce the possibility of wrong connections.

33.1.5 Pressure-Reducing Valve

A pressure-reducing valve is used to control the pressure to which a patient or piece of medical equipment is exposed when connected to a medical gas cylinder. Oxygen at 137 bar will severely damage an anesthesia machine and likely kill a patient if not regulated.

The most common type of pressure-reducing valve in anesthesia is the single stage reducing valve (◘ Fig. 33.8).

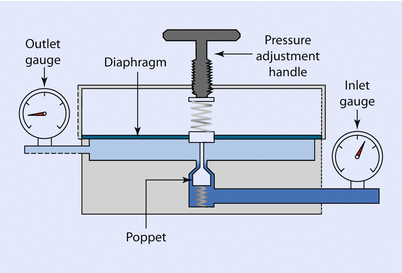
Fig. 33.8

Single-stage pressure reducing valve

In this valve, the inlet gauge is measuring the gauge pressure of the cylinder, in the case of oxygen, 137 bar when full. This pressure places a force on the diaphragm, which is displaced. A connecting rod from the diaphragm closes the poppet valve reducing flow from the cylinder, thereby regulating outlet pressure. The outlet pressure can be altered by relaxing or compressing the spring that is resisting diaphragm movement. This is done by turning the pressure adjustment handle. This valve is often incorporated as part of the yoke of the anesthesia machine in order to reduce cylinder gauge pressure to a working pressure that is safe for the equipment.

A 2-stage reducing valve may be found in certain gas delivery systems, such as an Entonox demand valve (◘ Fig. 33.9).

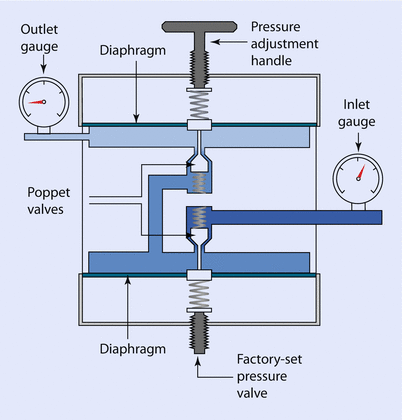
Fig. 33.9

Two-stage pressure reducing valve

This 2-stage valve usually has the second stage set so that gas only passes when the pressure is below atmospheric; i.e., when the patient draws on the mouthpiece. Firemen and airline pilots also use this type of valve in their respective breathing apparatus.

33.1.6 Pressure Transducers

A transducer is a piece of equipment that allows energy to be converted from one form into another. In the terms of a modern pressure transducer, the energy is converted from pressure to electrical energy and this is then displayed on a monitor, via software that converts the current to a displayed pressure reading. The conversion of energy takes place most frequently due to a strain gauge, which is a very small foil pattern on an insulating flexible backing, adhered to a flexible diaphragm that is distorted when exposed to pressure. The strain gauge is therefore also distorted and this results in a tiny but measurable change in its resistance. The change in resistance is usually measured using a circuit called a Wheatstone bridge, which, following amplification, offers sufficient sensitivity to be clinically usable.

One of the more common uses of a pressure transducer in anesthesia practice is the measurement of arterial blood pressure. The transducer is part of the arterial line and is exposed to the arterial pressure waveform via saline filled tubing. The resulting waveform and blood pressure values are displayed on a digital monitor.

33.2 Temperature

33.2.1 Definitions

Temperature is a measure of heat energy and defines whether an object will transfer heat energy to another object or, indeed, receive heat energy from another object. Heat is generated by an increase in the mean energy of the molecules that make up the object. As heat energy is applied to an object, its temperature obviously increases. If the object is then divided in 2, both parts will still have the same temperature (the same average kinetic energy of its constituent components), however, each half now has half of the heat energy of the original object.

There are 3 commonly used temperature scales: Fahrenheit, Celsius, and Kelvin. Americans and Europeans use the Fahrenheit and the Celsius scales respectively, with temperatures measured in degrees Fahrenheit (°F) or degrees Celsius (°C). The degree Kelvin (°K) is the SI unit of temperature and is used by the scientific community. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all thermal motion ceases in the classical description of thermodynamics. On the Fahrenheit scale, water freezes at a temperature of 32 °F and boils at 212 °F (at 1 atmosphere pressure). Absolute zero on this scale is not at 0 °F, but at −459 °F. Using the Celsius scale the freezing point of water is 0 °C and the boiling point is 100 ° C, while, absolute zero corresponds to a temperature of −273.15 °C. The relationship between the different scales is as follows:

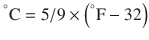
${}^{{}^{\circ}}\mathrm{C}=5/9\times \left({}^{{}^{\circ}}\mathrm{F}-32\right)$

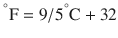
${}^{{}^{\circ}}\mathrm{F}=9/{5}^{{}^{\circ}}\mathrm{C}+32$

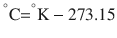
${}^{{}^{\circ}}\mathrm{C}{=}^{{}^{\circ}}\mathrm{K}-273.15$

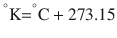
${}^{{}^{\circ}}\mathrm{K}{=}^{{}^{\circ}}\mathrm{C}+273.15$

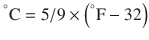
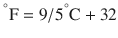
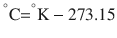
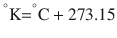
33.2.2 Temperature Measurement

Many methods are available for measuring temperature. The best way of classifying them is to divide them into those that use non-electrical methods and those that use electrical methods of measurement. Those that use non-electrical methods include the mercury or alcohol-filled glass thermometer, the bimetallic strip thermometer, and the Bourdon gauge thermometer. Electrical methods use 1 of 3 basic principles: the resistance thermometer, the thermistor, and the thermocouple. Infrared thermometers are also commonly used to record the temperature of hospital patients and also in the community. All of the electrical methods produce extremely small changes and employ a Wheatstone bridge circuit to make these small changes measurable.

The glass thermometer consists of a glass tube filled with mercury or some other liquid where a temperature increase causes the liquid to expand. The reading is then taken from the maximum point that the fluid has reached. A maximum reading thermometer has a small metal marker above the level of the mercury. Once the mercury has cooled and therefore contracted back down the thermometer, the metal marker remains at its maximum position and therefore indicates the maximum temperature reached. Mercury has historically been used in medical practice; however, this has almost been completely removed due to its toxicity. Alcohol sometimes replaces mercury in thermometers for measuring very low temperatures due to mercury solidifying at −39 °C. Alcohol, however, boils at 78.5 °C, so cannot be used in the higher ranges that mercury may be used.

A bimetallic strip thermometer uses 2 metals whose coefficients of linear expansion are different and are fixed together such that the composite bimetal assembly bends in proportion to temperature. If this is placed in a coil design, the deflection is amplified and a needle may be placed at the distal end of the strip causing a deflection on a scale.

A Bourdon gauge thermometer uses the principle of expansion of gases with increasing temperature (Charles’ law). The scale of the gauge displays temperature, but is truly a reflection of pressure.

The resistance thermometer consists of a length of fine coiled wire, often platinum, whose resistance increases linearly with temperature (◘ Fig. 33.10).

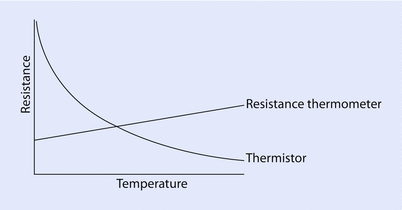
Fig. 33.10

Resistance changes based on temperature

A thermistor (“thermal resistor”) is an electrical resistor whose resistance varies inversely with temperature (◘ Fig. 33.10). It is usually based on a bead of a metal oxide.

A thermocouple consists of 2 dissimilar conductors in contact and is based on the principle that a junction of dissimilar metals will produce a temperature-dependent electric potential—a phenomenon known as the thermoelectric, or Seebeck, effect (◘ Fig. 33.11).

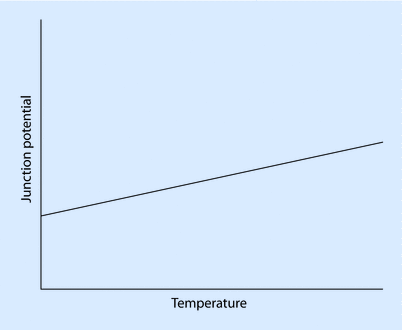
Fig. 33.11

The Seebeck effect

Temperature sensing chips (integrated circuit sensors) are popular in many applications because of their low cost, high degree of linearity, and relatively high voltage outputs.

Infrared thermometers determine the temperature of an object from a portion of the thermal radiation (“blackbody radiation”) emitted by the object. Contact with the object is not needed.

33.3 Gas Physics

33.3.1 Kinetic Theory of Gases

On the microscopic scale, gases are modeled by the kinetic theory of gases. This model assumes that the molecules have very small sizes relative to the distance between them and that the molecules are in constant, random motion (◘ Fig. 33.12) related to their kinetic energy, which is given by

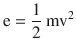$\mathrm{e}=\frac{1}{2}\ {\mathrm{mv}}^2$

where m is the mass of the molecules and v is its velocity.

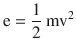
Fig. 33.12

The molecules frequently collide with each other and with the walls of the container holding the gas molecules. Like all molecules, gas molecules have physical properties of mass, velocity, momentum, and energy. At the macroscopic level these properties are related to properties of density, pressure, and temperature. The temperature of a gas is related to the mean kinetic energy of the gas; the higher the temperature, the greater the molecular motion.

33.3.2 Gas Laws

Air is a gas at standard temperature and pressure, and it is therefore important to understand the laws that govern its gaseous behavior. Gases are usually described in terms of pressure, volume, and temperature. Pressure is most often quantified clinically in terms of mmHg, cmH₂O, kPa, or bar, volume in ml, and temperature in degrees Celsius or Kelvin. Perhaps the most important law of gas flow in airways is the Ideal (or Perfect) Gas Law, which can be written as:

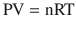$\mathrm{PV}=\mathrm{nRT}$

where

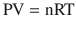
P = pressure of gas (Pascals or mmHg)
V = volume of gas (m³ or cm³ or ml)
n = number of moles of the gas in volume V
R = gas constant (8.3143 J g-mol⁻¹ K⁻¹, assuming P in Pascals, V in m³)
T = absolute temperature (in Kelvins or K, 273.16 K = 0 °C)

The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions and is derived from Avogadro’s law, Boyle’s law, and Charles’ law.

Avogadro’s Law

Avogadro stated that equal volumes of all ideal gases at the same temperature and pressure contain the same number of molecules. One mole is the quantity of a substance containing the same number of particles as there are in 0.012 kg of ¹²C. This number is 6.023 × 10²³ molecules and is called Avogadro’s number. One mole of an ideal gas takes up 22.4 litres at standard temperature and pressure (STP). STP may be defined as a temperature of 273.16 K at 1 atmosphere (760 mmHg).

Boyle’s law, which is the First Ideal Gas Law, states that, at a constant temperature, the product of pressure and volume is equal to a constant (◘ Fig. 33.13); that is:

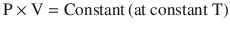$\mathrm{P}\times \mathrm{V}=\mathrm{Constant}\left(\mathrm{at}\ \mathrm{constant}\ \mathrm{T}\right)$

Hence, P is proportional to 1/V. Gases do not obey Boyle’s law at temperatures approaching their point of liquefaction (the state where the gas becomes a liquid). A simple application of Boyle’s law is the calculation concerning the contents of a cylinder of oxygen. If a 10 litre cylinder of oxygen is at a pressure of 137 bar (13,700 kPa), then this same quantity of gas at atmospheric pressure (100 kPa) will occupy 1370 litres.

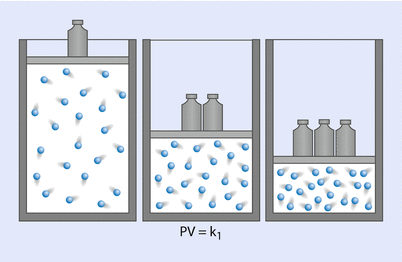
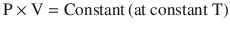
Fig. 33.13

Charles’ law states that, at a constant pressure, volume is proportional to temperature; that is, V is proportional to T (at constant P). See ◘ Fig. 33.14.

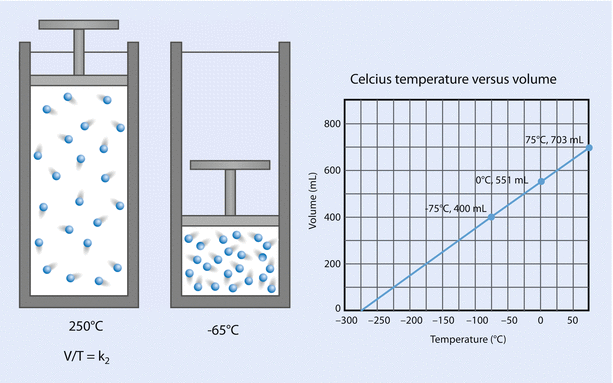
Fig. 33.14

Gay-Lussac’s law states that, at a constant volume, pressure is proportional to temperature; that is, P ∝ T (at constant V):

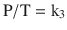
$\mathrm{P}/\mathrm{T}={\mathrm{k}}_3$

When a gas obeys both Charles’ law and Boyle’s law, it is said to be an ideal gas and obeys the Ideal Gas Law, PV = nRT, as previously described.

The aforementioned laws mandate the input or removal of heat energy to the system, however, the state of a gas can be altered without adding energy into the system. This is called an adiabatic process and is defined as a thermodynamic process during which no energy is transferred as heat across the boundaries of the system. An example of this is the rapid compression of a gas. This will cause a rise in temperature, requiring cooling. This is particularly relevant with respect to anesthesia. When an oxygen cylinder connected to the back of an anesthetic machine is turned on rapidly, the rapid compression of the gases in the connecting pipes and gauges causes an increase in temperature, with the consequent risk of fire.

We may also make use of this adiabatic process with an instrument called the Cryoprobe. This is an instrument that has an extremely cold tip, as low as −70 °C, and is used in dermatology, gynecology and ophthalmic surgery in order to rapidly freeze tissues. The principle of the Cryprobe is to allow the release and therefore rapid expansion of a gas, typically nitrous oxide or carbon dioxide, in the tip of a handheld probe. The rapid expansion of the gas causes a large fall in temperature as the energy to overcome the attraction between the molecules of the gas has to come from the kinetic energy of the molecules themselves.

33.3.3 Non-ideal Gases: The Van Der Waals Effect

Ideal gases are assumed to have no forces of interaction. Real gases, however, have intermolecular attraction, resulting in a weak force of attraction. This is called a Van Der Waals Force and requires that the ideal gas law be written as:

$\left[\mathrm{P}+\frac{{\mathrm{an}}^2}{{\mathrm{V}}^2}\right]\left(\mathrm{V}-\mathrm{nb}\right)=\mathrm{nRT}$

Where:

P = pressure of gas (pascals or mmHg)
V = volume of gas (m³ or cm³ or ml)
n = number of moles of the gas in volume V
R = gas constant (8.3143 J g-mol⁻¹ K⁻¹ assuming P in pascals, V in m³)
T = absolute temperature (K)
a, b = physical constants for a given gas

The terms a and b for a given gas may be found in physical chemistry textbooks and other sources. This formulation, provided by van der Waals, accounts for intermolecular forces fairly well.

33.3.4 Critical Temperature and Critical Pressure

Critical temperature is defined as the temperature above which a gas cannot be liquefied, regardless of the pressure applied to the gas.

For example, when preparing medical gases, oxygen will always be a gas at room temperature as its critical temperature is −119 °C. However, when a nitrous oxide cylinder is filled, there is a pressure at which the nitrous oxide is liquefied at room temperature; this is because the critical temperature of nitrous oxide is 36.5 °C.

The critical pressure of a gas is the vapor pressure exerted by a substance at its critical temperature.

The terms “critical temperature” and “critical pressure” apply to a single gas. When there is a mixture of gases, there is a temperature at which the gases may separate into their constituent components. This is termed the “pseudocritical temperature.” This is clinically important as Entonox may separate into oxygen and nitrous oxide at a cylinder temperature of −5.5 °C, which when opened may deliver a hypoxic mixture to a patient. The pseudocritical temperature of Entonox at pipeline pressure (50 PSI) is −30 °C, therefore it normally has no risk of separation in hospital pipelines.

33.3.5 Diffusion of Gases

Diffusion describes the process of the movement of molecules through a layer or surface. Clinically, diffusion of gases through a membrane is most applicable to gas flow across alveolar membranes. The most commonly used relation to govern diffusion is Fick’s first law of diffusion, which states that the rate of diffusion of a gas across a barrier is proportional to the concentration gradient for the gas. Fick’s law may be expressed mathematically as:

Only gold members can continue reading. Log In or Register to continue

Stay updated, free articles. Join our Telegram channel

Tags: Basic Sciences in Anesthesia

Dec 18, 2017 | Posted by admin in Uncategorized | Comments Off

Anesthesia Key

Fastest Anesthesia & Intensive Care & Emergency Medicine Insight Engine