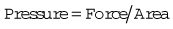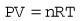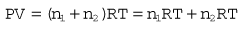Force, pressure and flow

Force is that which causes an object to move or, more accurately, to accelerate. Once it is moving, Newton’s Laws tell us that it will continue to move in a straight line at a constant rate unless some other force is applied to it. The SI unit of force is the Newton (N), which is defined as the force that causes a mass of 1 kg to accelerate by 1 metre per second per second (m s⁻²). Other units of force occasionally used are the kilogram force (kgf) and the pound force (lbf). These are forces equivalent to the force exerted by the earth’s gravity on masses of a kilogram and a pound, respectively.

Pressure is force per unit area over which the force acts, i.e.

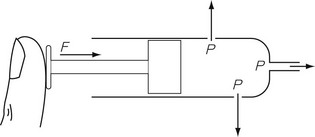
In any gas or liquid, pressure acts in all directions equally, whereas force acts in a given direction. For example, in a full hypodermic syringe, the liquid can be pressurized by applying a force to the plunger of the syringe. This is applied in the direction of travel of the plunger. However, if there were a leak in the barrel of the syringe, the liquid would squirt out sideways from the leak, as well as from the syringe outlet (Fig. 2.1), due to the pressure created by the force acting in all directions within the barrel of the syringe. The amount of pressure generated depends on the area of cross section of the barrel since it is over this area that the force acts. Thus, the pressure generated in a syringe with a small bore is higher than that generated in a syringe with a large bore for the same force applied to the plunger.

Figure 2.1 When the user exerts a force F on the plunger of an intravenous syringe, it is applied in one direction only, but the resulting fluid pressure P is exerted in all directions.

The SI unit of pressure is the Pascal (Pa), which is the pressure that results from the application of 1 N over an area of 1 m². Because a pressure of 1 Pa is rather small, gas pressures in anaesthesia tend to be measured in kPa. Other units of pressure that may be used in anaesthesia are pounds per square inch (psi) and bar (the pressure exerted by the atmosphere at sea-level, which is the result of the weight of atmospheric gasses bearing down on the surface of the earth).

Flow can result from differences in pressure. If a liquid or gas encounters a region in which one point has a higher pressure than another, then it will move away from the point of higher pressure towards that of lower pressure. That motion is flow. The commonest type of unit of flow encountered in anaesthesia considers the volume of flow of a liquid or gas in a given time. The SI unit is metres cubed per second (m³ s⁻¹). As this is very unwieldy, litres per second (l s⁻¹) or litres per minute (l min⁻¹) are normally used. Strictly, these units describe Volume Flow where it is assumed that that pressure and temperature are constant. It is useful to have a measurement of flow that is independent of pressure and temperature.

All the individual gas laws, i.e. Boyle’s Law, Charles’s Law and Gay Lussac’s Law, can be summarized in the equation below using the Ideal Gas Law which relates the pressure and volume of a given mass of gas to its temperature:

where P is the pressure of the gas, V its volume, T its temperature, R a constant and n the number of moles of gas present. Measuring the change in the number of moles (n) of a gas in a stream gives a measurement of the number of atoms moving in the flow and is called Molar or Mass Flow.

Atmospheric pressure and partial pressure

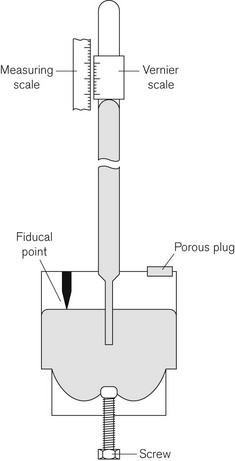
The definition of bar given above shows that the air exerts a pressure called atmospheric pressure. Atmospheric pressure is measured using a barometer, the simplest form of which is the Fortin barometer (Fig. 2.2). This consists of a long transparent tube, sealed at one end, which is filled with mercury and inverted with its open end in a bath of mercury exposed to atmospheric pressure. The atmospheric pressure acting on the surface of the mercury in the bath will support a column of mercury of about 760 mm above the surface of the mercury in the bath, leaving a virtual vacuum between the surface of the mercury in the tube and the sealed tube end. The height of column of mercury is measured using a Vernier scale at the top of the tube, which can be adjusted using a knob next to the barometer tube.

Figure 2.2 Fortin barometer. The level of the surface of mercury in the lower chamber is equilibrated to ambient pressure via the porous plug. The screw is adjusted until the surface of the mercury is touching the fiducal point. The level of the mercury in the column then represents the ambient pressure and is measured using the Vernier scale.

This measurement of atmospheric pressure leads to a further unit for pressure, millimetres of mercury (mmHg or Torr). If the tube of the barometer is 1 cm² in diameter, a column of mercury 760 mm high will weigh 1.033 kg, which means that atmospheric pressure is 760 mmHg = 1 bar = 1000 millibars = 15 psi = 1.033 kg cm⁻² = 1.01 × 10⁵ Nm⁻² = 101.3 kPa.

Partial pressure

Returning to the Ideal Gas Law (see above), it is clear that it makes no difference whether different gasses contribute the total number of moles present in any mixture of gasses. The Ideal Gas Law for a mixture of two gasses can be rewritten as:

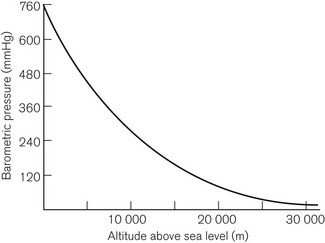
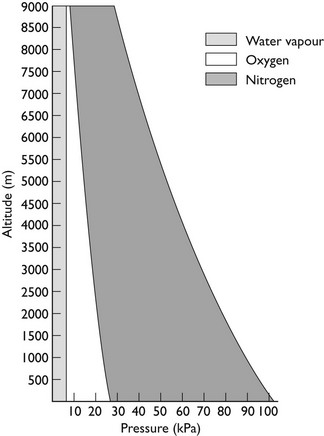
This is Dalton’s Law of Partial Pressures and shows that each gas exerts its own partial pressure independent of its companions. For example, if air is 20% oxygen and 80% nitrogen, then for an atmospheric pressure of 760 mmHg, the partial pressure of oxygen will be 152 mmHg and the partial pressure of nitrogen will be 608 mmHg. However, as Figure 2.3 shows, barometric pressure falls with altitude. Thus, when treating a patient at high altitude, a larger percentage of oxygen is required to supply the same partial pressure of oxygen. It is this partial pressure, not percentage of gas, which is clinically most important. The relationship between altitude and the partial pressure of the components of atmospheric air is shown in Figure 2.4.

Figure 2.3 The relationship between barometric pressure and altitude above sea level.

Figure 2.4 Variation with altitude of components of inspired air. Saturation with water vapour by upper airways is assumed.

Absolute, differential and gauge pressures

Since the barometer measures pressure with reference to effectively a vacuum, the measurement made is an absolute pressure measurement. There are other types of absolute measurements of pressure made with anaesthetic equipment. Mostly these are related to measurements of high pressures such as those encountered in gas cylinders.

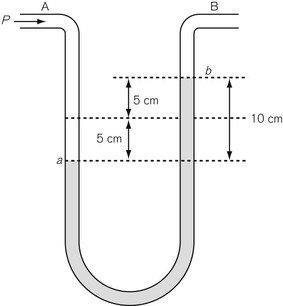
Differential pressure measurement is used where the difference in pressure between two points is required. The simplest differential pressure measurement system is the manometer, as shown in Figure 2.5. This takes the form of a U-shaped tube, partially filled with liquid such as water. Gas at pressure P is applied to end A, with end B open to the atmosphere (so having atmospheric pressure applied to it). The pressure at A causes water to be pushed to the other limb of the U so that the level in the right-hand limb moves to point b above where it was before the pressure was applied, and the water in the left-hand limb is depressed below its original level. If both move by a distance of 5 cm then the difference in water level created is 10 cm, indicating a pressure difference between A and B of 10 cmH₂O. Since the end B is open to atmosphere, the pressure at A can be thought of as being above atmospheric and is referred to as gauge pressure and is sometimes denoted by placing a ‘g’ after the pressure unit, e.g 10 cmH₂O g. If the ends A and B are at different points within a closed system, such as between the pleural cavity and the alveoli, then the pressure measured is a true differential pressure.

Figure 2.5 A simple manometer. A pressure P is applied at A. This causes a depression of the fluid level at a and a corresponding rise of the fluid level at b. In this case the tube is filled with water and the pressure is 10 cm of water.

Methods of measuring pressure

Mechanical methods

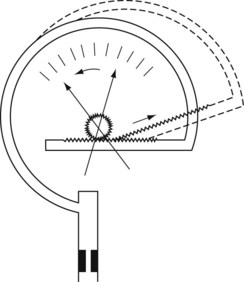
Bourdon gauge

The Bourdon gauge (Fig. 2.6) is robust, inexpensive and can withstand high pressures. It consists of a curved flattened tube, elliptical in section. When pressure is applied, the tube expands and in doing so attempts to straighten out. Levers, gears or a rack and pinion mechanism translate this movement to a dial pointer. The inlet has a constriction within it to protect the gauge from sudden increases in applied pressure. This gauge is normally used in anaesthesia to indicate cylinder and pipeline pressures. In this application, the pressures measured are much greater than atmospheric pressure. As the response to the applied pressure is determined by the mechanical properties of the Bourdon gauge tube, it effectively measures absolute pressure.

Figure 2.6 The principle of the Bourdon tube pressure gauge. Note the constriction at the inlet.

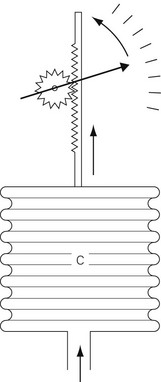
Aneroid gauge

The mechanical principles of an aneroid gauge are shown in Fig. 2.7. It measures absolute pressure and, as with the Bourdon gauge, the movement generated by application of pressure to a chamber is translated into movement of a dial by a mechanical linkage. The amount of movement generated is controlled by the compliance of the aneroid chamber so that the more rigid the chamber the higher the pressure that the gauge will indicate. The sensitivity of the gauge can be controlled by the gearing ratio of the rack and pinion. Where encountered in anaesthetic devices, aneroid gauges are relatively delicate and sensitive but able to indicate low pressures. They may be used to measure airway pressure or blood pressure. If the chamber is sealed and evacuated, the gauge becomes the familiar aneroid barometer. Electronic sensors of pressure have largely superseded the aneroid gauge.