, associated quantities are moment of inertia I, angular velocity 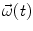 . The position vector
. The position vector 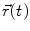 denotes the location of the centre of mass of a rigid body as function of time. Further quantities derived thereof are the velocity of the centre of mass
denotes the location of the centre of mass of a rigid body as function of time. Further quantities derived thereof are the velocity of the centre of mass 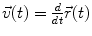 , and the acceleration
, and the acceleration 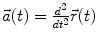 .
.
The linear motion of the rigid body is described by Newton’s second law of motion:
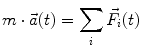
where the sum extends over all forces 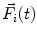 acting on the body. The spatial orientation of the body, in turn, is obtained from the angular momentum equation,
acting on the body. The spatial orientation of the body, in turn, is obtained from the angular momentum equation,
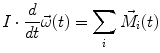
with the angular acceleration 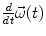 and the sum over all moments
and the sum over all moments 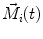 acting on the body. Because of the solidification principle, these equations also hold for deformable bodies, however, the centre of mass is not at a constant location with respect to the contour of the body in such cases. Variational principles, which can be derived within the framework of Newtonian mechanics, lead to Lagrange or Hamiltonian formulations which may be useful depending on the application under consideration.
acting on the body. Because of the solidification principle, these equations also hold for deformable bodies, however, the centre of mass is not at a constant location with respect to the contour of the body in such cases. Variational principles, which can be derived within the framework of Newtonian mechanics, lead to Lagrange or Hamiltonian formulations which may be useful depending on the application under consideration.
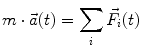
(2.1)
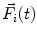 acting on the body. The spatial orientation of the body, in turn, is obtained from the angular momentum equation,
acting on the body. The spatial orientation of the body, in turn, is obtained from the angular momentum equation,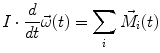
(2.2)
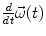 and the sum over all moments
and the sum over all moments 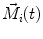 acting on the body. Because of the solidification principle, these equations also hold for deformable bodies, however, the centre of mass is not at a constant location with respect to the contour of the body in such cases. Variational principles, which can be derived within the framework of Newtonian mechanics, lead to Lagrange or Hamiltonian formulations which may be useful depending on the application under consideration.
acting on the body. Because of the solidification principle, these equations also hold for deformable bodies, however, the centre of mass is not at a constant location with respect to the contour of the body in such cases. Variational principles, which can be derived within the framework of Newtonian mechanics, lead to Lagrange or Hamiltonian formulations which may be useful depending on the application under consideration.Continuum mechanics: Basic quantities are field-oriented, viz., density 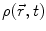 , time t, velocity field
, time t, velocity field 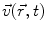 . The density
. The density 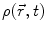 as well as the velocity field
as well as the velocity field 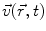 refer to a specific, fixed location
refer to a specific, fixed location 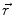 in space (this approach is often denoted as Euler representation of the continuum). The equation of motion reads (the independent variables are omitted for brevity)
in space (this approach is often denoted as Euler representation of the continuum). The equation of motion reads (the independent variables are omitted for brevity)
![$$ \frac{\partial }{\partial t}(\rho \vec{v}) + \left[ {\vec{v},\vec{\nabla }} \right] \cdot (\rho \vec{v}) = \vec{k} + \left[ {\vec{\nabla },\hat{\sigma }} \right] $$](/wp-content/uploads/2016/10/A82453_4_En_2_Chapter_Equ3.gif)
where 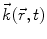 denotes field forces, e.g., gravity, while the stress tensor
denotes field forces, e.g., gravity, while the stress tensor 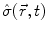 describes the internal state of loading (i.e., forces per unit area as normal and shear stresses) of the continuum and includes in addition forces which are due to external contact.
describes the internal state of loading (i.e., forces per unit area as normal and shear stresses) of the continuum and includes in addition forces which are due to external contact.  is the Nabla operator and vectorial quantities in brackets separated by comma denote a scalar product. The angular momentum relation requires that the stress tensor
is the Nabla operator and vectorial quantities in brackets separated by comma denote a scalar product. The angular momentum relation requires that the stress tensor 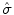 be symmetric. Conservation of mass furthermore yields the continuity equation
be symmetric. Conservation of mass furthermore yields the continuity equation
![$$ \frac{\partial }{\partial t}\rho + \left[ {\vec{\nabla },(\rho \vec{v})} \right] = 0 $$](/wp-content/uploads/2016/10/A82453_4_En_2_Chapter_Equ4.gif)
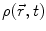 , time t, velocity field
, time t, velocity field 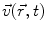 . The density
. The density 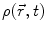 as well as the velocity field
as well as the velocity field 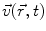 refer to a specific, fixed location
refer to a specific, fixed location 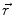 in space (this approach is often denoted as Euler representation of the continuum). The equation of motion reads (the independent variables are omitted for brevity)
in space (this approach is often denoted as Euler representation of the continuum). The equation of motion reads (the independent variables are omitted for brevity)![$$ \frac{\partial }{\partial t}(\rho \vec{v}) + \left[ {\vec{v},\vec{\nabla }} \right] \cdot (\rho \vec{v}) = \vec{k} + \left[ {\vec{\nabla },\hat{\sigma }} \right] $$](/wp-content/uploads/2016/10/A82453_4_En_2_Chapter_Equ3.gif)
(2.3)
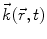 denotes field forces, e.g., gravity, while the stress tensor
denotes field forces, e.g., gravity, while the stress tensor 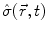 describes the internal state of loading (i.e., forces per unit area as normal and shear stresses) of the continuum and includes in addition forces which are due to external contact.
describes the internal state of loading (i.e., forces per unit area as normal and shear stresses) of the continuum and includes in addition forces which are due to external contact.  is the Nabla operator and vectorial quantities in brackets separated by comma denote a scalar product. The angular momentum relation requires that the stress tensor
is the Nabla operator and vectorial quantities in brackets separated by comma denote a scalar product. The angular momentum relation requires that the stress tensor 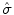 be symmetric. Conservation of mass furthermore yields the continuity equation
be symmetric. Conservation of mass furthermore yields the continuity equation![$$ \frac{\partial }{\partial t}\rho + \left[ {\vec{\nabla },(\rho \vec{v})} \right] = 0 $$](/wp-content/uploads/2016/10/A82453_4_En_2_Chapter_Equ4.gif)
(2.4)
These equations are non-linear and the velocity field can be obtained as a solution providing that the mechanical characteristics of the continuum in the form of a constitutive equation (see below) are introduced (a textbook on continuum mechanics is, e.g., Liu 2002).
In order to proceed, a distinction between a solid and a fluid continuum has to be made. In case of a solid, the velocity field follows readily from the displacements that the particles making up the continuum undergo as function of time. A wide variety of constitutive equations relating the displacements (or the deformations of the continuum resulting thereof) to the stress state can be found in the literature. For fluids, in turn, the stress tensor can be formulated in terms of the velocity field and its gradients.
While rigid body models are characterised by a finite number of degrees of freedom associated with a set of ordinary differential equations, in continuum mechanics partial differential equations prevail and the number of degrees of freedom is infinite. For numerical treatment, the partial differential equations have to be approximated in special formulations involving in particular discretisation, of which the finite element approximation is most often used in trauma biomechanics (see Sect. 2.7).
Constitutive Properties of Biological Tissues: Stress–strain characteristics of solid biological tissues are typically non-linear, anisotropic and visco-elastic. The non-linearity is mainly due to the large tissue deformations that are observed in biomechanics, the anisotropy to the fibrous character of biological tissues and the visco-elasticity to the internal friction inherent in the fibre-extracellular matrix composition. There are furthermore active elements (muscle fibres) whose tone influences the mechanical properties. In tests made under ex vivo conditions, the state of muscle activation has to be taken into account (muscle fibres can be activated chemically, e.g., by Barium compounds). Likewise, embalming of cadavers changes their mechanical behaviour. For biological fluids, non-Newtonian characteristics may be important (for a comprehensive treatment of constitutive properties in biomechanics see Holzapfel and Ogden 2006).
A distinction is often made in biomechanics between “soft” and “hard” tissues. In order to specify this difference more quantitatively, the non-linear, anisotropic, partly active (muscles) properties of biological tissues have to be characterised by a simplified linear approximation. Under uniaxial loading of a long and thin specimen, a piecewise linear stress–strain relation in the form of Hooke’s law can be adapted and a local modulus of elasticity or Young’s modulus E can be defined. For “soft” tissues, E varies typically between some 10 and 105 kPa, whereas the values for “hard” tissues are on the order of several GPa.
While there are numerous kinds of soft tissues, hard tissue in humans appears essentially in the form of calcified tissue, in particular bone. Thereby, the calcium is contained in hydroxyapatite crystals [Ca5 (PO4)3 OH] which are embedded in a collageneous matrix. Aside from the integrity and mechanical loading capacity of bones, a physiological calcium balance is eminently important for the overall homeostasis of the human body in that calcium is essential for many physiological processes, among them, the action of muscles, the transmission of nerve signals or the coagulation of blood. As such, calcium is by far the most abundant bone mineral material (“calcium reservoir”), others, e.g., phosphor, being much less concentrated. Therefore, the terms “calcification” and “mineralization” of bone are often used synonymously. Not surprisingly, bone mineral density (BMD) has been found to be a significant determinant with respect to fracture risk (Beason et al. 2003). Low calcium content in bones, as in the case of osteoporosis, increases the risk of bone fracture and lowers injury tolerance.
Essential constituents of soft tissues from a biomechanics’ point of view are elastin, collagen, and smooth muscle fibres. Modulus of elasticity (again under the simplified approximation of a piecewise linearised treatment of uniaxial loading) elastin (a globular, highly extensible polypeptide) has a Young’s modulus of 102–103 kPa, collagen (a stiff three-fold triple helix molecule) a Young’s modulus of up to 105 kPa, while smooth muscle fibres cover a wide range of stiffness characteristics between elastin and collagen depending on the state of activation. The anatomy of the organs consisting of soft tissue is mostly determined by their physiological function, therefore, according to the great variety of physiological functions, the composition of soft tissues varies greatly and so does their mechanical behaviour under load.
Bone, in turn, is less variable, although it exists in various forms: Cortical bone makes up the shaft (metaphysis) of the long bones as well as the outer layer of other bones while trabecular or cancellous bone is located mostly in the medullary canal of long bones, particularly in regions close to joints (epiphysis) as well as in the spine and in bones whose primary task is not to support loads (e.g., skull, iliac crest).
Since injury is basically associated with deformations beyond yield, linear approximations of the mechanical behaviour are generally questionable and great care has to be exercised when such procedures are applied. In reality, prior to irreversible, injurious tissue destruction, a mostly non-destructive, non-linear visco-elastic deformation behaviour sets in, followed by a plastic deformation phase. In soft tissues, plasticity is mainly due to an in general reversible rearrangement of tissue fibres. In the case of hard tissues, the processes underlying plastic deformation are less clear, they can however be visualised experimentally (Fig. 2.1). It has in fact been estimated that peak stresses in bone may significantly be reduced due to plasticity (Stitzel et al. 2003).
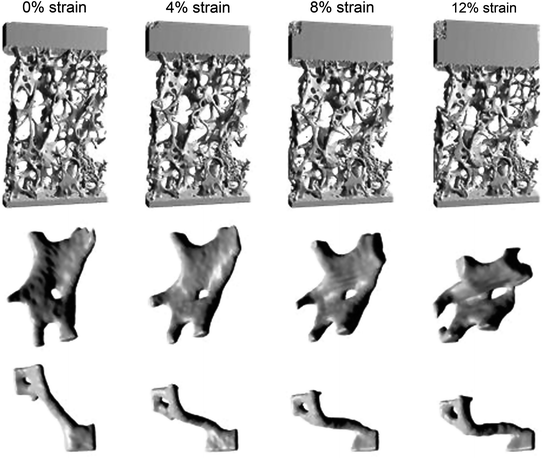

Fig. 2.1
Image-guided failure assessment of human spine samples with the aid of micro-CT (edge length of cross section 4 mm). The upper row exhibits a compressed specimen, imaged in steps of 4 % strain. The middle and lower rows show that the typical constituents of trabecular bone, viz., plates and rods, respectively, can undergo large plastic deformation before ultimate failure. Since the basic material of bone, i.e., hydroxyapatite crystals in a collageneous matrix is the same also in cortical bone (although the microstructure is quite different), local plastic deformation may also occur in cortical bone sections under load (From: R. Müller et al. Functional Microimaging at the Interface of Bone Mechanics and Biology, in: Holzapfel and Ogden, op. cit.)
Age dependence of constitutive properties is prominent. While soft tissues in young children are highly deformable, with increasing age, stiffening sets in. This effect is mainly due to decreasing water content and increasing fibre cross-linking. While the total body water during adolescence amounts up to 70 % body weight, it decreases down to almost 50 % in old age. The younger a child, furthermore, the more bendable a bone is because of the gradual development of mineralisation. Accordingly, fractures denoted as “greenstick” fractures are observed in children in contrast to adults where fractures tend to exhibit a more brittle appearance.
Two major failure criteria are often applied in general mechanics in that it is assumed that failure sets in if a limit value of one of the following parameters is exceeded:
absorbed energy (von Mises criterion, applied in trauma biomechanics, e.g., in the thorax).
shear stress (criterion according to Tresca, usually not applied in trauma biomechanics).
In trauma biomechanics, in addition, the following quantities are used for the formulation of failure criteria, i.e., onset of injury (see Sect. 2.3), viz.
acceleration (applied, e.g., in head injury).
deformation (applied, e.g., for the assessment of bone fractures).
2.3 Injury Criteria, Injury Scales and Injury Risk
Injury criteria are important tools to assess the severity of accidental loading and the risk of sustaining injury thereof. By definition, an injury criterion correlates a function of physical parameters (e.g., acceleration, force) with a probability of a certain body region to be injured in a specific fashion (e.g., concussion, fracture). Injury criteria are generally derived from experimental studies in combination with empirical evidence, and their formulation and validation requires an extensive stepwise extrapolation procedure, since, as mentioned above, experiments on living humans at traumatic levels are excluded.
First, in addition to the concept of “injury criterion”, two further expressions have to be introduced, viz., “damage criterion” and “protection criterion”. While an injury criterion is intended to describe the property with respect to injury tolerance of living tissue, a damage criterion normally relates to post mortem test objects as surrogates for the living human. In both cases, a threshold value for the exposure to a quantity calculated from physical parameters is established above which, i.e., if the exposure exceeds the threshold, the test tissue in question is injured with respect to its anatomical or physiological structure in a specific fashion in more than 50 % of all experiments made or accidental exposures under comparable conditions. A protection criterion is obtained when postulating a threshold value on the basis of measurements performed with an anthropomorphic test device (see Sect. 2.6.1) as a human surrogate. In the latter case, the relation to human injury tolerance levels is mainly derived from empirical investigations. It is thereby assumed that a healthy middle-aged adult does on average not sustain injuries of the kind addressed by the particular criterion if he or she is exposed to loading conditions which are comparable to the ones defined in the protection criterion. The actual risk of injury can then be estimated with a risk function which relates the probability to be injured to the criterion developed (i.e. the underlying mechanical properties measured). A threshold value is defined such that, given a certain loading scenario represented by a certain value for the criterion, the risk of sustaining injury does not exceed a percentage of 50 %. Depending on the type of injury, this threshold may also be selected at a lower value of e.g. 20 %.
However, the definitions of injury, damage, and protection criteria are often not clearly differentiated and thus the term injury criterion is widely used for any index meant to quantify impact or accidental loading severity. Protection criteria, in turn, are determined in internationally standardised test procedures, mostly for use in automotive laboratories. These procedures are listed in Sect. 2.6. In the Chaps. 3–8 specific injury criteria for each body region are presented.
Scales to classify the type of an injury are based on medical diagnosis and were developed for injuries sustained in traffic accidents. The most widely used such scale is the Abbreviated Injury Scale (AIS), which was first developed in 1971 as a system to define the severity of injuries throughout the body and which is regularly revised and up-dated by the Association for the Advancement of Automotive Medicine (AAAM). AIS is a standardised system for categorising the type and severity of injuries arising from vehicular crashes (Table 2.1) and is oriented towards the survivability of an injury, i.e., each category represents a certain threat-to-life associated with an injury. Thus, AIS is an anatomically based, global severity scoring system that classifies each injury in every body region by assigning a code which ranges from AIS0 to AIS6. Higher AIS levels indicate an increased threat-to-life. AIS0 means “non-injured” and AIS6 “currently untreatable/maximum injury”.
Table 2.1
The AIS classification
AIS code | Injury |
|---|---|
0 | Non-injured |
1 | Minor |
2 | Moderate |
3 | Serious |
4 | Severe |
5 | Critical |
6 | Untreatable |
As a result, the AIS severity score is a single, time independent value for each injury and every body region. The severity is described regarding its importance to the whole body, assuming that the described injury occurs to an otherwise healthy adult. However, it has to be noted that the AIS considers only the injury and not its consequences. Clinical complexity, cost of surgical treatment, and long-term sequelae are in particular not taken into account. Hence, severe impairments such as loss of eyesight or life-threatening complications due to nosocomial infections occurring in a hospital are not coded as severe injuries, because they do not represent an initial threat-to-life.
Moreover, the AIS code is not a linear scale in the sense that the difference between AIS1 and AIS2 is comparable to the one between AIS5 and AIS6. It does therefore not make sense to calculate average AIS codes (AIS 3.7, e.g., is a meaningless number). To describe an overall injury severity for one person with multiple injuries, the maximum AIS (MAIS) is used. The MAIS represents the highest AIS code sustained by one person on any part of the body, even if the person in question sustained several injuries of the same severity level at different body parts. If, for example, a car occupant sustained AIS2 injuries on the head and the legs but no injuries classified higher, the MAIS will still be MAIS2.
To account for a better representation of patients with multiple injuries, the Injury Severity Score (ISS) was introduced which is regularly updated like the AIS scale (latest version: AAAM 2005 Update 2008). The ISS distinguishes six different body regions: head/neck, face, chest, abdomen, extremities including pelvis, external (i.e. burns, lacerations, abrasions, and contusions independent of their location on the body surface). For each of these regions the highest AIS code is determined. Then the ISS is calculated by the sum of the squares of the AIS codes of the three most severely injured body regions. Thus the minimum ISS is 0 and the maximum ISS is 75 (i.e. three AIS5 injuries). If an AIS6 injury is recorded, the ISS is automatically assigned to 75. ISS values higher than 15 are regarded as major trauma. Several studies have shown that the ISS correlates quite well with several measurement systems such as mortality (e.g. Baker and O’Neill 1976) or long-term impairment (e.g. Campbell et al. 1994). However, there are also limitations associated with the ISS such as the maximum of three contributing injuries. Consequently an further developments like the New Injury Severity Score (NISS) as well as other injury scales were presented (see e.g. Chawla et al. 2004).
In addition to the AIS, other scales are used to specify injuries of particular body regions in more detail. The Quebec Task Force (Spitzer et al. 1995), for example, established a scaling scheme to categorise soft tissue neck injuries (see Chap. 4). A classification scheme for head injuries often seen in emergency medical reports is the Glasgow Coma Scale (GCS) (Teasdale and Jennett 1974). GCS aims at describing the state of consciousness and some neurological signs (e.g. reflexes) of the injured person after a traumatic incident, and may thus allow the inclusion/exclusion of potential injury mechanisms. The scale ranges from 3 (deep coma) to 15 (fully awake).
Further scales address impairment, disability and societal loss through ratings of the long-term consequences of the injury by assigning an economic value. An example is the Injury Cost Scale ICS (Zeidler et al. 1989), by which the average costs for an injury is determined taking into account the costs for medical treatment and rehabilitation, loss of income and disability. Further economic scales are the Injury Priority Rating IPR (Carsten and Day 1988) and the HARM concept (Malliaris 1985) applied by the US government. One of the most crucial problems in trauma biomechanics is the assessment of the relationship between injury severity and a mechanical load which causes this injury, i.e. to find a relationship that allows assigning probabilities which describe the likeliness that a certain mechanical load (e.g. determined by an injury criterion) will cause a particular injury. This is important because without such correlations, it is useless trying to interpret any results obtained, for instance, in crash tests. Hence, it is necessary to perform well-equipped laboratory experiments using human surrogates to determine the biomechanical response and corresponding injury tolerance levels and consequently establish so-called injury risk functions.
For the determination of injury risk curves basic statistical methods are applied of which the maximum likelihood method, the cumulative frequency distributions, and the Weibull distribution are most often used. In Chap. 3, an example with respect to head injury is presented. For in-depth information however with respect to the application of statistical methods to the often complex and difficult analysis of accident and injury data the reader is referred to statistical text books. Great care has to be exercised in such analyses; among the various problems which may arise when transforming experimental results to (real world) injury risk functions, are
a small number of tests performed,
differences in the biomechanical response between the human surrogates used in testing (e.g. cadavers) and living humans,
anthropometric differences between the test subjects and the real world population at risk,
a large spread of data due to different test conditions used by different researchers,
a large number of possible injury mechanisms and injuries that might occur.
Basically the same limitations apply when using data from accident statistics instead of experimental results to fit injury risk curves. Nonetheless, decades of trauma biomechanics’ research have provided a sufficiently large number of sources that allow establishing a number of well-founded relationships that link mechanical loads to injury probability—at least for certain injuries and injury mechanisms, respectively. However, work is this area is by far not finished and revisions of existing criteria on the basis of new findings are not uncommon.
2.4 Accident Reconstruction
The reconstruction of accidents is an indispensable procedure in the field of trauma biomechanics because relations between loading and injury under physiological conditions manifest themselves only in real-life accidents. Likewise, accident reconstructions are often required for forensic purposes likewise in criminal and in civil cases.
The reconstruction of an accident consists of the mathematical analysis of the event in question on the basis of the laws of classical mechanics as outlined in Sect. 2.2. Other than laboratory experiments, however, accidents in everyday life occur under largely uncontrolled and unmonitored conditions. Depending on the extent, quality and accuracy of the available documentation, therefore, the specialist in accident reconstruction has to apply assumptions and approximations at quite different levels of complexity. While an accident in a skiing competition may be covered by various video recordings or the traces in a traffic accident may accurately be documented by the police, a fall from a ladder during household activities is hardly documented. All information is of importance in a reconstruction process. Much as in a puzzle, various sources of information have to be combined in order to produce a reliable and conclusive account of the events; this may include facts as different as the sequence of traffic lights in a vehicle–pedestrian impact and the bending stiffness of a pole in case of a sports incident. A scrutiny of the accident scene is always indispensable. Experience from formerly performed tests under laboratory conditions or the results from well documented “comparable” accidents may furthermore be of help. Of paramount importance is often the collaboration with the medical forensic expert in that injury patterns may provide useful clues for the purpose of accident reconstruction; for example, from the particular appearance of street dirt under the skin, the direction of a fall can be deduced.
Missing documentation or missing visible evidence may pose problems in accident reconstruction. In case of vehicle collisions, uncertainties might arise e.g. if due to anti-locking systems no skid marks are produced. Furthermore, reconstruction becomes more difficult when no or only marginal vehicle deformation occurs. In order to reduce the repair cost, modern vehicles are designed such that in collisions of low intensity nearly no damage is caused (or at least it is not visible from the outside and therefore often mistaken as not existing by laymen). However, missing visible damage does neither mean that there was no collision at all nor that the energy transmitted might not have been sufficient to cause injury to the occupant.
Within the framework of a rigid body approximation (Eqs. 2.1 and 2.2) for the description of an impact event, empirical investigations and laboratory experiments have shown that the acceleration of the centre of mass experienced by a body limb under the influence of impact forces is an important parameter to assess the severity of an impact. In many practical cases, the modulus of the acceleration is thereby often related to the acceleration due to gravity, g (1 g = 9.81 m/s2), because we are constantly exposed to gravity such that we can relate a given acceleration level to everyday experience. Yet, the acceleration which a body undergoes during the course of an accident varies with time, such that the quantities “peak acceleration” and “mean acceleration” along with the corresponding intervals in time should always be clearly distinguished in order to prevent misunderstandings.
Reconstruction techniques have mostly been developed systematically for traffic accidents. In such cases, a number of specific parameters relating to an involved vehicle have found to be useful for an assessment of the loading situation of occupants.
The collision or impact velocity of a vehicle is probably the parameter most frequently quoted in the public. In accident reconstruction, the travelling speed or, more accurately, the speed before the beginning of any braking action, is sometimes of importance when investigating whether or under which circumstances a collision could have been avoided, or whether a speed limit was exceeded.
The collision-induced velocity change (delta-v) of the vehicle under consideration is, however, in most cases more useful for describing the collision severity where the effects of the collision on the occupants are concerned. The delta-v corresponds approximately to the integral of the translational vehicle deceleration over the collision time for collisions which are characterised by a single impact without significant rotation of the vehicle. Yet, in complex collision situations (roll over, fall over the roadside, etc.) delta-v may not be a well-defined parameter.
The energy equivalent speed (EES) characterises the amount of energy needed to deform a vehicle. In fact, the EES represents the impact velocity into a rigid barrier that would have been necessary to cause the same permanent deformation as observed in the real world accident. The EES is given in [km/h] and can be obtained for many vehicle types from so-called EES catalogues. These catalogues are established on the basis of crash tests conducted under well-defined test conditions.
A further parameter used to describe impact conditions is the vehicle overlap. This is the extent to which the vehicle and the collision partner (e.g. another vehicle or a barrier in a crash test) overlap. The overlap is generally presented as the percentage of the total width of the vehicle under consideration covered by the opposing vehicle (or wall).
From basic mechanics, the principles of elastic and plastic impact and the accompanying coefficient of restitution (k-factor) are used to characterise the elastic and plastic (i.e. permanent) components of the deformation suffered in the impact. Figure 2.2 shows, as an example, the dependency of the coefficient of restitution on the impact velocity (against a rigid wall). The k-factor heavily depends on the design of the car front structure, in particular the bumpers and underlying absorbers for low-energy collisions. Due to the requirements for no or little dam-age cost in these collisions, bumpers have been designed to be stiffer and more elastic, thus, for newer cars, higher coefficients of restitution must be assumed in the low-speed area. Furthermore, some impact absorber concepts involve designs or materials whose deformation recovers slowly after an impact. Since this restitution does not occur during the impact itself, the vehicle deforms in a fully plastic way although the accident investigator may not find any deformation after the collision.
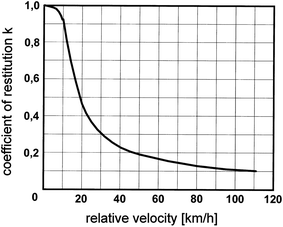
Fig. 2.2
Schematic representation of the relation between the coefficient of restitution and the relative velocity for a frontal impact on a rigid barrier for a passenger car [adapted from Appel et al. 2002]. Newer cars will generally exhibit higher coefficients of restitution in the low-speed range than shown in this figure
Today, most traffic accident reconstructions are performed with facilitating computer programmes which mainly employ rigid body dynamics (Eqs. 2.1 and 2.2). Using such programmes, two methods can be distinguished in principle: “forward” and “backward” calculation. In the first case, the kinematics before the collision are assumed, i.e. initial directions of motion, velocities etc. are assigned to the collision partners. Then, the actual collision and the final positions of the collision partners after the collision are determined by integration of the rigid body equations taking into account tyre and collision forces. Finally, the positions and traces that were recorded on the actual accident scene are compared with the results of the calculation. In an iterative process, the input parameters are adjusted and the procedure is repeated until a satisfactory match between the results obtained in the calculation and the available accident data is reached. The backward calculation method starts by investigating the final positions of the collision partners. Next, the motions after the impact are reconciled with the traces found (e.g. skid marks) giving the positions at impact, again utilizing rigid body approximations. Eventually, the initial parameters that lead to the determined course are obtained. Graphics are finally used to give a visual account of the reconstructed accident.
Because of the large mass ratio car occupant/vehicle, the influence of car occupants, likewise of other objects which are not rigidly connected with the vehicle can be taken into account in an approximate fashion. This is not the case in motorcycle or bicycle accidents, where the programmes mentioned above can only be applied under restricted conditions and the results have to be interpreted carefully.
Collision phases, not only in traffic accidents, are usually associated with deformation processes for which the application of approximations based on continuum mechanics (Eqs. 2.3 and 2.4 and associated constitutive relations) are required. Because of liability issues mostly, car manufacturers are reluctant to publish the finite element models which they use to assess the crashworthiness of their vehicles. Various types of simplification are therefore made in general purpose reconstruction programmes. One way is to assume a segmented stiffness distribution of the vehicle’s front, and then to integrate the equations of motion of the two vehicles over the collision duration. Another way, often employed in European reconstruction programmes, is to assume the collision duration to be infinitely short (in comparison to the pre- and post-crash motion of the vehicles) and to calculate only the transfer of the (linear and rotational) momentum from one vehicle to the other. The EES values mentioned above may, for both approaches, be used as control values to obtain not only conservation of momentum, but also the energy balance over the collision.
Once a vehicle motion is reconstructed, the motion of the occupants or of an impacted external victim (pedestrian, two-wheeler) during impact can be estimated, again using rigid body models. Furthermore, indications with respect to the occupant loading can be obtained. Further extrapolations, in particular concerning injuries, however require expertise beyond the classical (mechanical) accident reconstruction. The same holds true for accidents occurring at the workplace, household or in sports. Given appropriate circumstances and a careful adaptation to the situation in question, traffic accident reconstruction models and computer programmes can also be utilised in other accidents. For the purpose of injury analysis, the subsequent application of a finite element model of the human body may yield useful clues.
Finally, accidents are sometimes reconstructed by a one-to-one reproduction on location or in the laboratory with the original installations, vehicles, sports accessories, etc. This procedure is particularly important in non-traffic related accidents as well as in the course of legal procedures where large claims justifying the often considerable expense of such tests are involved.
2.5 Experimental Models
All mechanical characteristics relating to the behaviour in time of the human body, of a part of it, of an organ or tissue when it is subjected to dynamic mechanical loading is subsumed under the term “biomechanical response”. The head-neck kinematics as observed in a rugby scrummage or the force–deflection characteristics of the chest due to a frontal vehicle impact are examples for the biomechanical response of the human body. Besides such mechanical changes, the biomechanical response can also lead to physiological changes like neck pain, oedema of the lung or aberrations of the ECG.
A thorough knowledge of the biomechanical response is indispensable for the development of measures for injury prevention and mitigation. Since accident situations as such are highly dynamic by their nature, relevant tests to investigate the biomechanical response of the human body have generally to be conducted under corresponding loading conditions. Nevertheless, whenever extrapolations to dynamic conditions are possible, quasi-static tests are made because of the much simpler installations needed for such tests.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree







